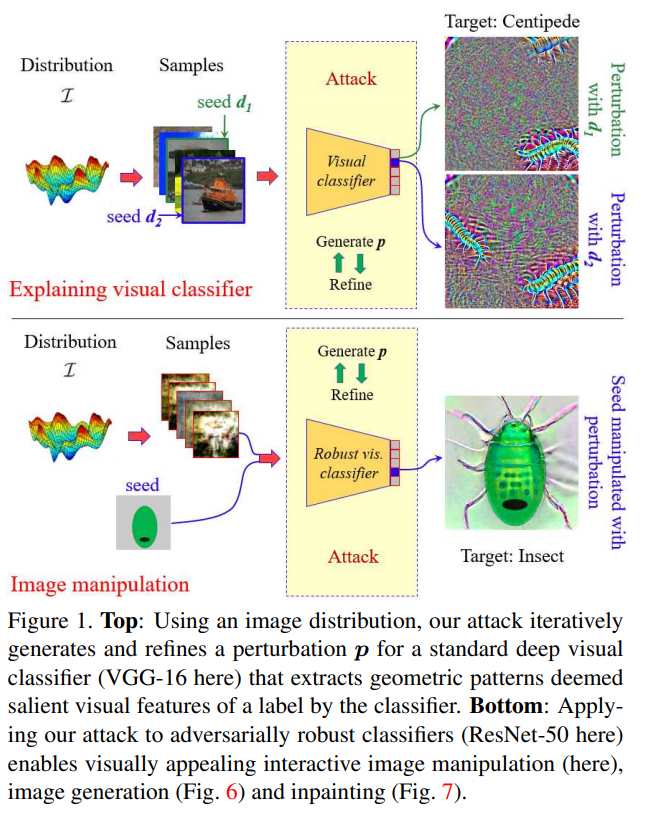
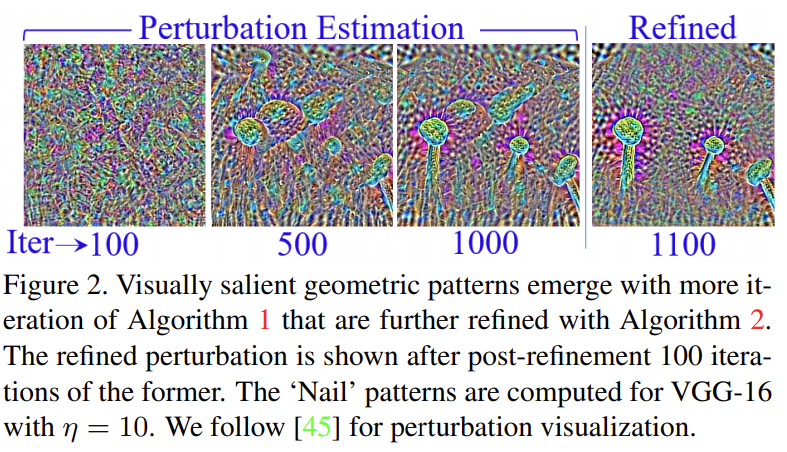
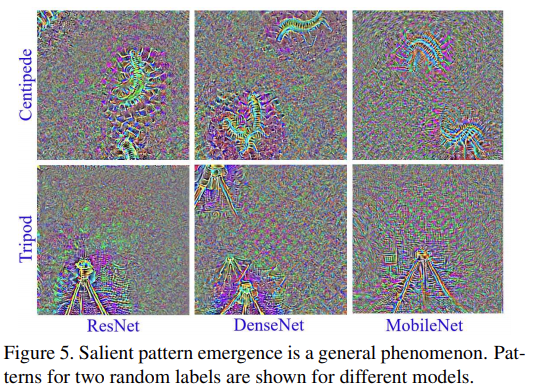
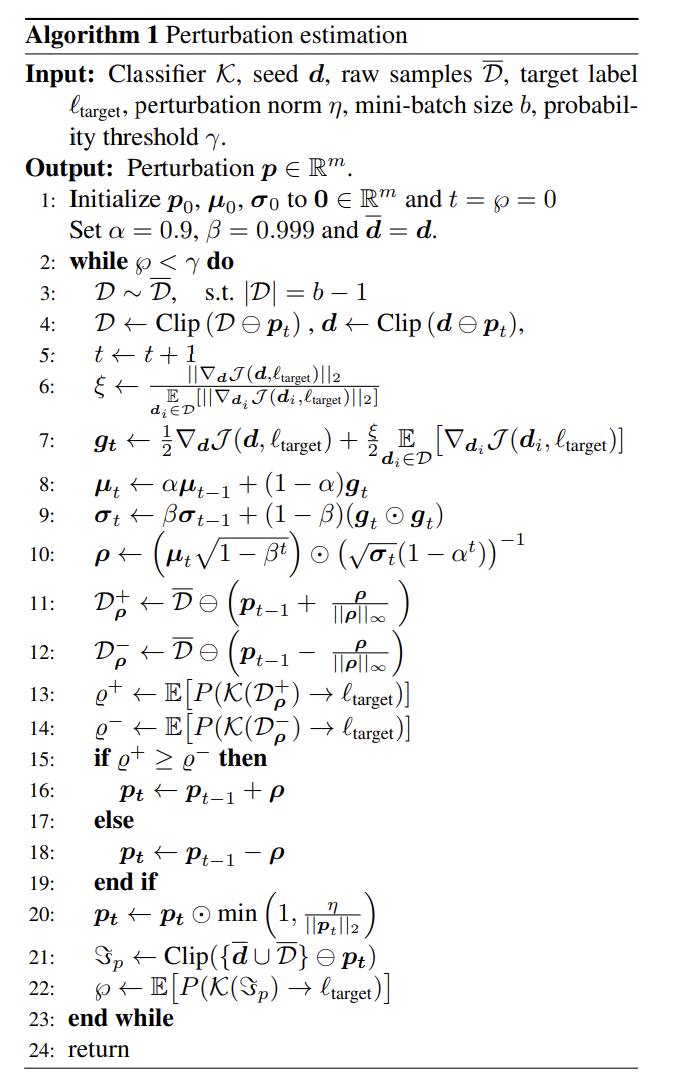Loss Function Search for Face Recognition

Abstract

AutoML로 인해 성능좋은 AM-LFS 것처럼 hand-crafted loss function은 sub-optimal이다. 본 논문은 softmax probability를 줄이는 것에 집중하여 margin-based softmax loss function을 만든다.

1. Introduction

Face Recognition은 얼굴을 구별하는 Face identification과 얼굴을 비교하는 Face verification이 있다. 여기서 loss function이 큰 역활을 한다. 크게 contrastive loss와 triplet loss와 같은 metric learning loss function와 classification loss function이 있다. metric learning loss function은 계산량이 많으며, 비교대상이 되는 샘플에 대해 성능에 큰 영향을 받는다.

직관적으로, face features은 intra-class compatness와 inter-class separability가 크면 클수록 더 쉽게 구분할 수 있다. 그래서, 기존의 softmax loss가 face features를 잘 구분하지 못한다는 말이 많았다. center loss와 몇몇의 softmax loss의 진화는 intra-class variance를 줄였으며, A-Softmax는 inter-class variance를 줄였다. 그러나 위의 방법들은 조심스럽게 파라미터들을 조정해야지 최적의 결과가 나온다. 또한, AM-Softmax loss나 Arc-Softmax와 같이 기하학적인 loss function도 있지만, 매우 큰 design space를 거쳐야하며 일반적으로 sub-optimal에 도달한다.

최근 AutoML을 통해 AM-LFS라는 loss function search method가 발표되었다. 이 논문은 loss funtion의 hyper-parameter를 매개변수화된 확률 분포 샘플링을 공식화하고 여러 vision task에서 좋은 결과를 가져왔다. 하지만, 이 방법은 intra-class distnace에서 inter-class distance의 상대적 중요성을 활용하여 탐색 공간의 디자인을 이끌어내는데 사용하지않아, 결과적으로 복잡하고 불안정하다.

따라서, 위의 단점을 보완하기위해 기존의 hand-crafted loss function의 장점들을 분석하여 적용해 더 효과적인 방법을 제안한다.

• "어떻게 하면 softmax probability를 줄일 수 있을까?"에 대해서 생각을 했다.
• 단순하지만 매우 효과적인 search space를 설정했으며, random/reward-guided method를 사용했다.
• LFW, SLLFW, CALFW, CPLFW, AgeDB, CFP, RFW, MegaFace 와 Trillion-paris 등등 많은 벤치마크에 대해서 비교 실험을 했다.

2. Preliminary Knowledge

softmax: softmax function + cross-entropy loss로 만들어져있으며, 밑의 수식과 같다.

face recongnition으로 오게되면 weights $w_k$와 feature $x$로 정규화되고 scale parameter $s$로 magnitunde가 대체되며 밑의 수식과 같아진다. 여기서 cosine similarity($cos(\theta_{w_k,x}) = w_k^Tx$)가 추가되어 face recognition의 구별성을 증가시켜준다.

Margin-based Softmax: 여러 margin이 추가된 loss function이 생겨났으며, A-softmax loss, Arc-softmax loss 그리고 AM-Softmax loss가 유명하다.

전체적으로 $f(m, \theta_{w_y},x)<cos(\theta_{w_y},x)$인 margin function을 가진다. 각각,

• A-Softmax loss: $f(m_1, \theta_{w_y},x)=cos(m_1\theta_{w_y},x)$ 와 $m_1\geq1$
• Arc-Softmax loss: $f(m_2, \theta_{w_y},x)=cos(\theta_{w_y},x + m_2)$ 와 $m_2>0$
• AM-Softmax loss: $f(m_3, \theta_{w_y},x)=cos(\theta_{w_y},x)-m_3$ 와 $m_3>0$
• 위의 것을 합친 loss: $f(m, \theta_{w_y},x)=cos(m_1\theta_{w_y},x + m_2) - m_3$ 존재한다.

AM-LFS: AutoML for Loss Function Search의 약자로 search space를 설정해 loss function을 찾는 논문이다.

$a_i$와 $b_i$는 search space의 매개변수이며 $i \in [0, M-1]$에 따라 사전에 분할된 softmax probability의 bin이다. M은 bin의 갯수를 나타낸다. 결과적으로 search space는 조각별 선형 함수(piece-wise linear function)를 사용하는 후보 집합으로 볼 수 있다.

3. Problem Formulation

본 논문에서 저자들은 margin-based softmax losses를 공식화하고 무작위성을 가진 reward-guided loss function search method를 만들었다고 합니다.

3.1 Analysis of Margin-based Softmax Loss

먼저 softmax probability를 다음과 같이 정의 한다.

그리고 margin-based softmax probability $p_m$은 다음과 같다.

위의 수식과 같이 유도되며 변조 인자인 $a$는 음수의 값을 가진다. ($a\leq0$)

표 1에 요약되어 있으며, $a=0$일 때, margin-based softmax probability $p_m$은 softmax probability $p$와 같다. 즉, 위의 $h(a,p)=\frac{1}{ap+(1-a)}\in (0,1]$로 모든 softmax probability를 표현할 수 있으며, 어떻게 하면 softmax probability를 줄일 수 있을까에 대한 답을 찾을 수 있을 것이다.

AM-LFS와 차별성이 3가지가 있다. 1) 본 논문의 수식인 $p_m$이 항상 softmax probability$p$보다 항상 작지만, piece-wise linear function 은 그렇지 않다. 즉, AM-LFS가 변별력을 항상 보장하지는 않는다. 2) 본 논문의 수식은 하나의 매개변수 $a$를 가지지만, AM-LFS는 2M개를 가진다. 즉, AM-LFS가 복잡하고 불안정하다. 3) 본 논문의 수식은 매개변수의 타당한 범위를 가지지만, AM-LFS는 제한이 없다.

3.2 Random Search

위의 분석을 그대로 수식 (2)에 넣어 통합된 공식을 만들었으며, 다양한 classes 사이에서 구별성 feature의 능력을 가질 수 있겠했다. 또한, search space를 $h(a, p)$로 정의할 수 있게 된다.

각 train epoch에서 변조 인자 $a\leq0$를 무작위로 설정하고 Random-Softmax로 표기한다.

3.3 Reward-guided Search

softmax probability를 줄일 수 있다면, feature discrimination이 강화되는 것으로 볼 수 있다. 하지만, 학습을 하는데 어떤 가이드라인이 없다면 최적은 아니다. 따라서, 이 문제를 해결하기위해 hyper-parameters $B={a_1,a_2,...,a_B}$ 로 각 학습 epoch의 분산을 주고 현재 모델을 학습하는데 사용한다. hyper-parameter $a$는 가우시안 분산을 이용한다.

1번의 학습이 완료된 뒤, B 모델들은 생성되고 이 모델의 reward $\mathcal{R}(a_i),\ i\in [1,B]$는 hyper-parameter $\mu$의 분산을 업데이트한다.

여기서 $g(a_i);\mu, \sigma$는 가우시안 분포의 PDF이다. 위의 방식으로 a의 분산을 업데이트하며 B의 후보들중 다음 epoch에 사용할 최고의 모델을 찾는다. 이것을 Search-Softmax라고 부른다.

3.4 Optimization

여기서는, Search-Softmax loss의 학습 과정을 보여준다. network model $\mathcal{M}_w$가 있다고 할 때, training set $\mathcal{S}_t = {(x_i, y_i)}_{i=1}^n$와 validation set $\mathcal{S}_v$ 각각에 대해 search loss는 최소화 하면서 rewards인 $r(\mathcal{M}_{w*(a)}, \mathcal{S}_v)$를 최대화 하는 것을 목표로 한다. 즉,

과거 논문에 의하면, 변조 인자 $a$가 hyper-parameter로 있다면, standard bi-level optimization problem(표준 이중 수준 최적화 문제.,..?)로 볼 수 있다. 즉, 내부적으로는 loss $L^a$를 최소화하는 매개변수 $w$를 학습하면서, 외부적으로는 테스트 셋인 $S_v$에 대해 rewards를 최대화 하는 weight $w^*$를 찾는다. 마지막에는 재학습 없이 사용하며, 문제를 단순화하기위해, 표준편차는 고정하고 평균은 최적화 했다. 밑의 알고리즘 1에서 확인할 수 있다.

4. Experiments

4.1 Datasets

** Training Data: CASIA-WebFace, MS-Celeb-1M Test Data: LFW, SLLFW, CALFW, CPLFW, AgeDB, CFP, RFW, MegaFace, Trillion-Pairs. Dataset Overlap Removal.**: open-set evaluation에서 training/test set 간의 겹치는 사람이 있으면 안된다. 따라서, 저자들은 CASIA-WbeFace에서 696명/ MS-Celeb-1M-v1c에서 14,718명을 제거하여 training set으로 사용했다. 표2에서 확인할 수 있다.

4.2 Experimental Settings

Data Processing.

• detect: Face-Boxes detector
• localize: 6-layer CNN
• crop size: 144x144 and RGB
• normalize: (x - 127.5) / 128
• horizontally flip (a=0.5)

CNN Architecture. SEresNet50-IR을 사용해 512-dimension feature을 얻는다.

Training. Inner level과 outer level을 구분해서 구현 했다.

1. Inner level: model parameter $w$를 최적화 한다.

• SGD optimizer
• batch size: 128
• weight decay: 0.0005
• momentum: 0.9
• learning rate: 0.1 ( [9, 18, 26] divide 10) - CASIA-WebFace-R(30) 0.1( [4, 8, 10] divide 10)- MS-Celeb-1M-v1c-R(12)

2. outer level: 변조 인자 $a$를 REINFORCE로 최적화 한다. 여러 샘플들로 부터 model parameter $w^*$를 찾는 방법이다.

• Adam optimizer
• learning rate: 0.05
• 분산: 0.2
• 최적의 mean을 찾는다.

Test. 위에 제시된 dataset에서 테스트를 진행하며 original image를 사용하였다.

• Face identification: Cumulative Match CHaracteristics (CMC)
• Face verification: Receiver Operating Characteristic (ROC) 를 사용했다.

낮은 false acceptance rate (FAR)에서 true positive rate (TPR)이 강조 되는데, 실제로 false accept 보단 false rejection이 더 낮은 risk를 제공하기 때문이다.

대망의 비교 metric들은, Softmax, A-softmax, V-Softmax, AM-Softmax, Arc-Softmax 그리고 AM-LFS이다.

• AM-LFS를 제외하고는 paper에서 그대로 가져와 사용했다.
• AM-LFS는 직접 재구현하여 최고 좋은 성능을 가져와 사용했다.
• V-Softmax는 batch size와 virtual classes를 같게 함.
• A-Softmax는 $m_1=3$으로 설정함.
• Arc-Softmax와 AM-Softmax는 각각, $m_2=0.5\quad m_3=0.35$로 설정함.
• scalie parameter $s$는 32로 고정하여 사용함.

4.3 Ablation Study

Effect of reducing softmax probability.

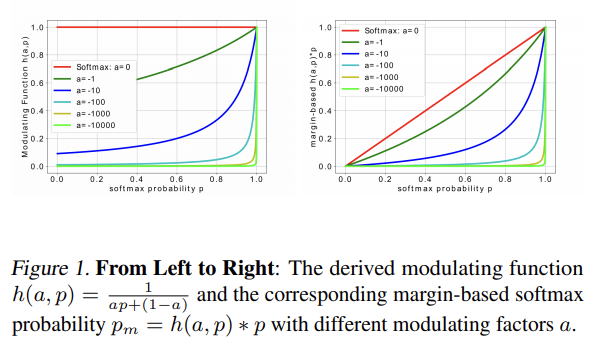
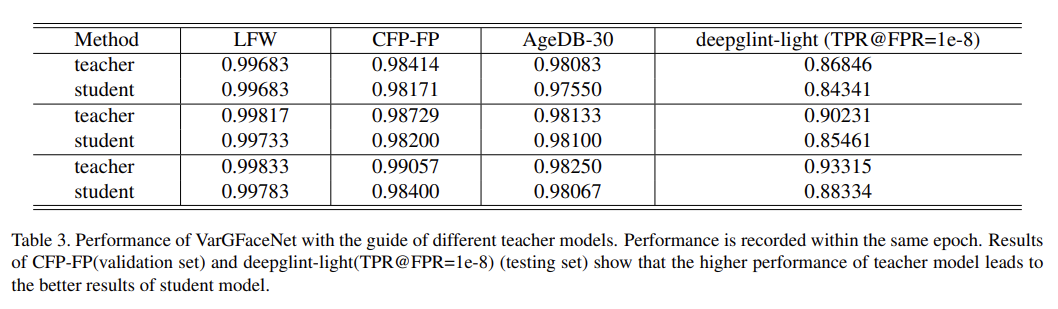
여기서는 변조 인자에 따른 softmax probability가 줄어듬에 따른 영향을 연구한다. $h(a,p)$는 단조증가함수 인데, 이것으로 인해 $p_m=h(a,p)*p$는 항상 softmax probability보다 작은 0~1사이의 값을 가지게된다. 게다가, 표3의 LFW와 SLLFW을 보면 softmax probability가 줄어들면, 성능이 증가하는 것을 확인할 수 있다. 결국, softmax probability가 줄어드는 것이 feature discrimination을 강화시켜주는 것으로 볼 수 있다.

Effect of the number of sampled models.

매개변수 $B$를 변경해가면 Search-Softmax loss를 찾았다. $B={2,4,8,16}$이며 표4에서 결과를 확인할 수 있다. B의 값에 따라 다르긴 하지만, 최적의 샘플을 찾는냐 못찾는냐의 차이인 것같다. 따라서, 저자들은 $B$를 4로 고정해서 학습을 진행하였다.

Covergence.

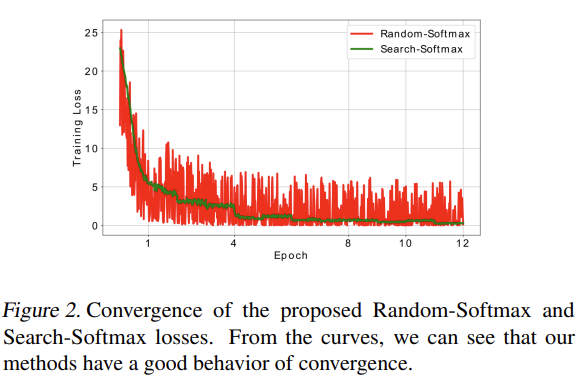
위의 방법들이 수렴하는 것이 이론적으로 분석하기 어렵지만, 경험적으로 수렴한다는 것을 알 수 있다. 그림 2를 보면 들쑥날쑥하지만, 수렴해 가는 것을 볼 수 있다. 명백하게 epochs이 증가할 수록 loss가 감소하며 성능이 올라가고 있다. 매개변수 $\mu$는 최적 분포를 향하고 있으므로 각 epoch에 대해 샘플링된 $a$는 더 나은 성능을 달성하기 위해 loss value를 줄이는 방향으로 간다.

4.4 Results on LFW, SLLFW, CALFW, CPLFW, AgeDB, CFP

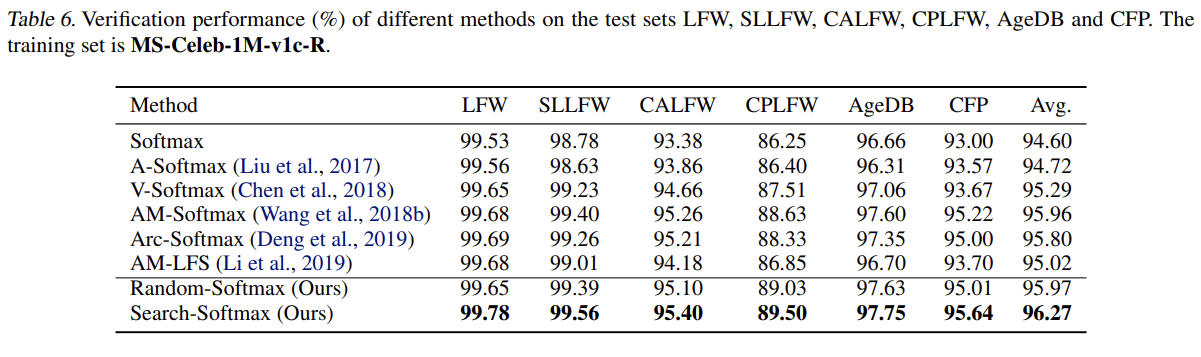
전체적으로 좋은 성능을 보이며, Random-Search-Loss가 생각보다 좋은 성능을 보인다. 본 논문의 최적화 전략은 dynamic loss가 다른 epochs에서 사용할 수 있기 때문에 discrimination power을 더욱 높이는데 도움이 된다. 하지만, 위의 데이터셋은 포화상태여서 새로운 데이터셋이나 새로운 방법을 찾아야한다.

4.5 Results on RFW

최근의 새로운 데이터 셋인 RFW에 대해 테스트를 진행했으며, racial bias를 측정하기위한 데이터셋이다. 4개의 데이터셋으로 Caucasian, Indian, Asian 그리고 African으로 이뤄져있다.

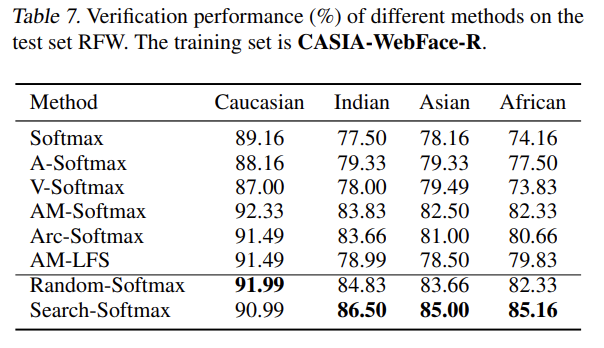
본 논문의 방법이 baseline보다 더 좋은 성능을 가져오며, 이것을 토대로 softmax probability가 줄어들면, 얼굴인식에 필요한 식별력(discrimination power)이 강화되는 것을 알 수 있다.

4.6 Results on MegaFace and Trillion-Pairs

MegaFace: identification TPR@FAR=1e-6 verification TPR@FAR=1e-6 Trillion Pairs: identification TPR@FAR=1e-3 verification TPR@FAR=1e-9

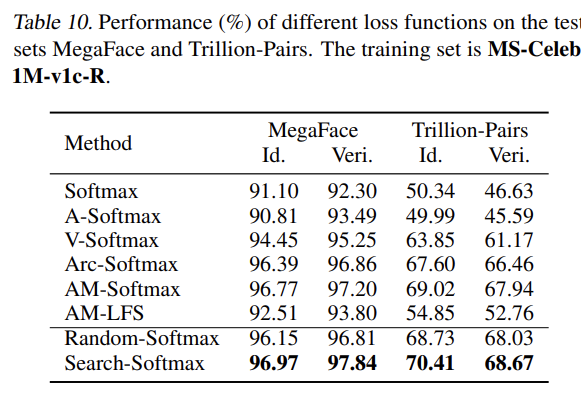
본 논문에서 제시하는 Search-Softmax가 모든 baseline보다 더 좋은 성능을 보인다.

또한, MegaFace set 1에 대해 CMC curves (identification) 와 ROC curves (verification) 를 보여준다.

Trillion-Pairs Challenge와 MegaFace test set에 대해 비슷한 trends을 볼 수 있다. 즉, Search-Softmax loss가 face recognition task에 대해 큰 일반화를 보여준다고 할 수 있다.

5. Conclusion

본 논문은 얼굴인식에 필요한 식별력을 강화하는 방법이 softmax probability를 줄이는 것이라고 한다. 이러한 정보를 근거로 random-softmax / Search-Softmax를 구현했으며, softmax baseline들 보다 더 좋은 성능을 가져왔다.

Revisiting ResNets: Improved Training and Scaling Strategies

I. Bello W. Fedus X. Du E. Cubuk ...

Abstract

Novel Computer vision architecture들은 spotlight를 독점하지만, 모델 구조의 영향력은 보통 학습 방법과 scaling strategies의 변화와 함께 융합된다. 본 논문은 ResNet을 가지고 3가지 측면에서 위의 내용을 풀어낸다. 놀랍게도, training과 scaling 전략들이 구조를 바꾸는 것보다 더 좋은 결과를 가져왔다. 최고의 성능을 가지는 scaling strategy를 보여줄뿐만 아니라, 2가지의 새로운 scaling strategies를 제안한다. 1) overfitting이 발생할 수 있는 영역에서 model depth scaling. 2) 추천된 방법이 아닌 좀 더 느리게 image resolution을 증가시키는 것.

본 논문에서는 ResNet을 개선하여 ResNet-RS를 제안한다. TPU에서 EfficientNet보다 1.7~2.7배 더 빠르며 비슷한 정확도를 가지며 large-scale semi-supervised learning setup에서 Top-1 86.2%의 정확도를 가진다. 본 저자들은 새로운 ResNet을 실제로 사용하는 것을 추천한다.

1. Introduction

vision model의 성능은 모델구조, 학습 방법과 scaling 전략의 생성물이다. 하지만, 최근 연구들은 구조 변경만 강조하며, novel architecture들이 많은 발전의 기초가 되지만 동시에 학습 방법과 hyperparameters들을 변경해야하는 부분들이 있다. 최신의 학습방법으로 새로운 구조를 학습한 것들도 때지난 학습방법으로 오래된 구조와 비교를 자주한다. (ResNet과의 비교). 본 논문은 유명한 ResNet 구조의 학습방법과 scaling 전략의 영향력에 대해 연구한다.

먼저, ResNets에 적용된 최근 학습방법과 정규화 방법에 대해서 조사했으며 표 1에서 볼 수 있다. 학습방법 사이의 상호작용을 발견했으며, 여러개의 정규화 기술을 사용할 때, weight decay value를 줄이면 이득을 보는 것을 확인했다. 표 1에서도 확인할 수 있는데, 개선된 학습 방법으로 약 3%의 성능 상승을 확인했으며, 2개의 작고 공통적인 구조인 ResNet-D와 Squeeze-and-Excitation을 추가해 성능 상승을 확인했다.

본 논문에서는 철저하게 scaling rule들을 정해 진행했는데, 모든 학습 기간을 철저하게 지켰다. (10 epoch 대신에 350 epoch 사용). 여기서, 저자들은 모델크기, 데이터셋 크기, epoch의 수와 같은 scaling strategy와 학습 영역과 최고 성능 사이의 의존성을 발견했다. 또한, 이러한 의존성은 작은 영역에서는 누락되었으며 이것은 sub-optimal이 나타나게했다. 따라서, 저자들은 새로운 scaling stragies를 제안했으며, 1) overfitting이 발생할때는 depth를 늘리는 것을 멈추고 width를 늘리기 2) image resolution을 천천히 증가시키기 이다.

이러한 학습 및 scaling strategies를 사용해 ResNet-RS를 만들었으며, EfficieintNet보다 더 빠르고 성능이 좋다. 특히, large-scale semi-supervised learning setup에서는 더 큰 차이를 보였다.

마지막으로, 개선된 training과 scaling strategis의 전략의 일반성을 테스트하는 일련의 실험으로 마무리한다. 먼저 저자들의 방법으로 EfficieintNet-RS를 만들어 일련의 downstream takss에서 최신의 self-supervised algorithms (SimCLR SimCLRv2)와 비교했으며, video classification으로도 확장이 가능하다. 약 3D-ResNets으로 Kinetics-400 dataset에 대해 약 4%의 성능 향상을 보았다.

Contributions

• 정규화 기술와 그것들의 상호작용을 실험을통해 최적의 상태를 찾았으며 이것은 모데 구조 변경없이 이뤘다.
• 쉬운 scaling stragy를 제안함.1) overfitting이 발생할때는 depth를 늘리는 것을 멈추고 width를 늘리기 2) image resolution을 천천히 증가시키기
• ResNet-RS: TPU에서는 EfficientNet보다 1.7~2.7배 GPU에서는 2.1배~3.3배 더 빠르다.
• Semi-supoervised training에서 EfficientNet-NoisyStudent보다 TPU에서 4.7배 (GPU에서 5.5배) 더 빠르며 86.2%를 달성함.
• self-supervised representations(Sim-CLR와 SimCLRv2)에서도 좋은 성능을 보임.
• 3D resNet-RS로 video classification으로 확장을 했으며, baseline보다 약 4.8% 성능 향상을 보임.

2. Characterizing Improvements on ImageNet

AlexNet이후로 image recognition 분야는 발전해왔는데 크게 4가지 분야로 발전되었다. 네트워크 구조, 학습/정규화 방법론, scaling strategy 그리고 추가적인 학습 데이터 사용

Architecture. novel architectures이 큰 관심을 받아왔다. AlexNet을 시작으로 최근에는 NAS를 활용한 네트워크들이 있다. 또한, adapting self-attention을 visual domain에 적용하여 이미지 분류 를 위한 ConvNets에 영향을 주거나 lambda layers와 같은 대안을 사용하는 방법들도 있다.

Training and Regularization Methods. ImageNet의 등장은 학습과 정규화 접근의 혁신을 앞당겼다. dropout, label smoothing, stochastic depth, dropblock 그리고 data augmentation과 같은 정규화 방법이 있으며, learning rate schedules로 정확도를 개선한 방법들도 있다. 하지만, RegNet과 같이 작은 데이터셋에서는 좋은 성능을 보이지만, ImageNet과 같은 큰 데이터 셋에서 좋은 성능을 보이는지 확인하지않은 연구들도 있으며, 작은 데이터셋에서 성능이 좋다고 해도 더 큰 규모에서 개선이 있는지 불분명하다.

scaling Strategies. 모델의 dimensions (width, depth and resolution)을 증가시키는 것은 확실히 성능 향상을 기대할 수 있다. NLP 영역의 GPT-3나 Switch Transformer의 성능 향상이 이를 증명 했으며, 비슷하게 computer vision 분야에서도 유용성을 증명했다. ResNet 같은 경우 depth를 증가시키며 width를 증가시킨 논문들도 있다. 최근 학습 budgets이 증가함에 다라 resolution을 600이나 448로 사용하는 논문들도 있으며, 이것을 compound scaling rule로 체계화한 EfficientNet이 있다. 그러나, 이러한 scaling strategy는 ResNet 뿐만 아니라 EfficientNet 또한 sub-optimal에 도달하도록 한다.

Additional Training Data. 추가적인 데이터를 학습에 사용하여 정확도를 올리는 방법은 유명하다. 최근에는 130M개의 unlabeled images에 psuedo-labels를 사용해 정확도를 올린다. Meta pseudo-labels는 semi-supervised learning technique의 개선된 방법인데, ImageNet에서 약 90% 성능을 가져왔다. 이는 ResNet-RS에도 적용했으며 밑의 표4에서 확인할 수 있다.

3. Related Work on Improving ResNets

개선된 학습방법과 구조 변경을 통해 성능향상은 항상 이뤄져왔다. stem과 downsampling block을 수정하는 반면 label smoothing과 mixup을 사용한 논문들도 있다. 또한, SE block 추가, selective kernel, 그리고 anti-alisa downsampling을 사용한 논문도 있다. 최근에는 여러 구조 변경과 개선된 학습 방법으로 EfficientNet-B1~EfficientNet-B5까지 따라잡은 연구도 있다.

위의 연구들은 scaling strategies에 신경을 쓰지않는 반면 본 논문은 조그마한 구조 변경과 training/scaling strategies에 집중한다. 따라서, 앞서 언급한 방법들과 매우 다른 방법이며, 추가적인 요소로 예측한다.

4. Methodology

4.1 Architecture

크게 2가지의 구조 변경이 있는데, ResNet-D와 모든 bottleneck에 SE Block을 추가하는 것이다.

ResNet-D은 총 4가지의 수정사항이 있다.

1) Inception-V3와 같이 stem의 $7\times7$ convolution을 3개의 $3\times3$으로 변경한다.

2) downsampling blocks의 residual path에서 처음 2개의 convolution에 대한 stride size 전환

3) downsampling blocks의 skip connection path에서 stride-2 $1\times1$ convolution을 $2\times2$ average pooling과 non-stride $1\times1$ convolution으로 바꾼다.

4) stride 2 $3\times3$ max pool layer를 제거하고 그 다음 bottleneck block에 $3\times3$ convolution을 추가한다.

밑의 그림 6에서 변경 사항을 확인할 수 있다.

Squeeze-and-Excitation은 전체 feature map에서 average pooling signals로 cross-channel interactions을 통해 channel의 가중치를 재설정하는 것이다. 하지만, 본 논문에서 SE block을 쓰지 않은 경우도 있으며 따로 명시해두었다.

4.2 Training Methods

정규화와 data augmentation methods에 대한 연구이다.

Matching the EfficientNet Setup. 350epoch을 쓰는 것 처럼 EfficientNet의 학습 방법과 비슷하지만 다른점이 3가지가 있다. 1) cosine learning rate schedule 사용(<-> exponential decay) 2) RandAugment 사용 (<-> autoAugment) 3) Momentum optimizer (<-> RMSProp)

Regularization weight decay, label smoothing, dropout 그리고 stochastic depth를 사용함. Dropout의 경우 마지막 layer에서 grobal average pooling이후 출력에서 사용함. Stochastic depth는 층의 깊이에 따라 특정 확률로 각 layer을 제거하는 기술이다.

Data Augmentation. RandAugment를 사용하며, 일련의 random image transformations로 data augmentation을 적용한다. AutoAugment보다는 성능이 조금 더 좋다.

Hyperparameter Tuning. 본 논문에서는 ImageNet training set의 2%를 held-out validation set으로 사용하며, minival-set과 validation-set이 존재한다. 하이퍼 파라미터는 밑의 표 8에서 확인할 수 있다.

5. Improved Training Methods

5.1 Additive Study of Improvements

ResNet-200은 기본적으로 79.0%의 정확도를 가지는데 개선된 학습 방법을 사용하면 82.2% (+3.2%)의 향상이 있으며, SE block과 ResNet-D를 사용하면, 83.4% 까지 상승한다. 개선 된 학습 방법으로 3/4의 성능 향상을 볼 수 있었다.

5.2 Importance of decreasing weight decay when combining regularization methods

table 2는 여러 정규화 방법을 조합하여 사용할 때, weight decay를 바꾸는 것에 대한 중요성을 보여준다.

보는 것과 같이 RandAugment와 label smooting만 사용했을 때는 괜찮지만 더 추가적인 방법을 적용하면, 오히려 성능이 떨어진다. 직관적으로, weight decay가 regularizer로 사용됨을 알 수 있다. 최근 논문에서 추가적인 data augmentation은 가중치의 L2 norm을 감소시킨다고 주장하는 논문도 있으며, 여러 논문에서 더 작은 weight decay를 사용하면 성능이 올라감을 나타낸다.

6. Improved Scaling Strategies

multipliers에 따라 다르게 학습을 시켰다. Appendix E 에서 확인할 수 있다. width = [0.25, 0.5, 1.0, 1.5, 2.0] depth = [26, 50, 101, 200, 300, 350, 400] Resolution = [128, 160, 224, 320, 448] 을 적용했다.

FLOPs do not accurately predict performance in the bounded data regime (FLOPs은 제한된 데이터 영역에서 성능을 정확하게 평가할 수 없다.)

위의 그림에서 보이는 것처럼 작은 모델은 error와 FLOP 영역 사이에 어떤 법칙이 있는 것 처럼 보인다. 하지만, 더 큰 모델에서는 그 법칙이 소용이 없어진다. 즉, 무조건 크다고 좋은 성능을 가져오는 것이 아님을 확인할 수 있다. 따라서, 원하는 FLOPs내에서 정확한 scaling configuration이 필요하다.

The best performing scaling strategy depends on the training regime. (최고 성능 scaling strategy는 학습 체제에 따라 다르다.)

따라서, FLOPs에 따른 정확도 비교가 아닌 speed-accuracy Pareto curve을 사용한다. 그림 3에서 확인할 수 있다.

위의 그림을 보면 확연하게 최고의 성능을 가지는 scaling을 확인할 수 있다.

6.1 Strategy #1- Depth Scaling in Regimes Where overfitting can Occur

Depth scaling outpeforms width scaling for longer epoch regimes. (긴 epoch에서는 width scaling보다 depth scaling이 더 나은 성능을 보인다.)

그림 3의 right를 보면, width scaling에서 성능 저하가 나타난다. 이것은 overfitting을 뜻하는데, width scaling이 더 많은 파라미터를 사용하기 때문이다. 즉, depth scaling은 width scaling보다는 적은 파라미터 증가를 가진다.

Width scaling outperforms depth scaling for shorter epoch regimes. (더 짧은 epoch에서는 width scaling이 더 나은 성능을 보인다.)

반대로, 그림 3의 left를 보면, width scaling에서 더 좋은 성능을 보인다. 또한, 그림 3의 middle을 보면, depth scaling과 width scaling이 서로 다르게 차이나는데 input resolution에 따라 다른다. 이와 같은 결과는 training 영역에서 scaling strategy가 항상 같은 규칙을 가지지않음을 보인다. 이는 과거의 연구들에서도 비슷한 결과를 보이는데, 더 짧은 epoch에서는 너비를 조정하는 것이 바람직하다는 실험 결과와 일치한다.

6.2 Strategy #2 - Slow Image Resolution Scaling

위의 그림 2를 보면 더 큰 image resolutions는 오히려 성능이 감소한다. 따라서, 과거의 연구들은 600 심지어 800의 resolution을 가지지만, 이거와 반대로 천천히 증가시켜야한다고 생각한다. Section 7.2에서 더 자세히 설명한다.

6.3 Two Common Pitfalls in Designing Scaling Strategies

scaling strategy에 대한 연구로 과거의 scaling straegy에 대한 2가지 헛점을 발견했다.

(1) Extrapolating scaling strategies from small-scale regimes. 작은 모델이나 작은 epoch에서 만든 scale rule은 잘못되었다고 생각하며, 일반화가 덜 된 것으로 판단한다. 과거의 연구들은 작은 모델 또는 짧은 training epochs로 scaling rules를 주장햇는데, 이것은 best performing scaling strategy와 training regime 사이의 의존성을 누락시켰다. 즉, 더 큰 모델이나 epoch에서는 scaling rule이 깨진다.

(2) Extrapolating scaling strategies from a single and potentially sub-optimal initial architecture. (최적화되지 않은 single initial architecture에서 scaling strategies 추정) 최적화 되지 않은 초기 구조로 부터 시작하는 것은 scaling results를 삐뚤어지게할 수 있다. 예를들어, EfficientNet-B0는 고정된 FLOPs와 resolution에서 찾은 네트워크 구조인데, 이것은 거기에 해당하는 FLOPs와 resolution에 국한되어 있다. 반대로 본 논문은 다양한 widths, depths 그리고 resolution에서 디자인했다.

6.4 Summary of Improved Scaling Strategies

새로운 task를 할 때, 모델을 다른 scales에 따라 작은 subset으로 나눠 full training epochs로 실행하는 것을 추천한다. 물론, cost가 많이 들지만, 제일 좋은 architecture을 찾을 수도 있다.

이미지 인식 분야를 위해 scaling stategies는 1) overfitting 발생 전까지 depth를 늘리고 2) resolution을 천천히 키우는 것이다. 이러한 방법으로 ResNet-RS와 EfficientNet-RS를 발견했다. 비슷한 사례로 LambdaResNets와 NFNets가 있다.

7. Experiments with Improved Training and Scaling Strategies

7.1 ResNet-RS on a Speed-Accuracy Basis

개선된 training and scaling strategies를 사용해 ResNets을 재디자인한 ResNet-RS를 만들어 냈다. 그림 4에서 보는 것 처럼 speed와 accuracy가 훨씬 빠르다.

FLOPs vs Latency.(작은 파라미터와 크기를 가진 네트워크가 왜 더 느린가?) 예전부터 FLOPs가 실제로 학습및 평가 지연시간 측정을 하지못한다는 논문이 나왔따. 즉, FLOPss가 poor proxt라는 것이다. FLOP은 연산이 종종 메모리 접근 비용에 의해 제한되고 최신 행렬 곱 단위에서 다양한 수준의 최적화를 가지기 때문에 특히 좋지 않은 proxy이다. inverted bottleneck을 사용한 EfficientNet은 큰 활성화함수와 함께 depthwise convolutions을 실행하고 따라서 작은 활성화와 함께 dense convolution인 ResNet의 bottleneck 구조보다 메모리당 계산 비율이 적을 수 밖에 없다. -> 아마도... depthwise 방법은 한 depth당 메모리 access가 필요해서 실제로 지연시간을 줄인다는 것 같다. 밑의 표3은 이러한 부분을 나타내는 표이다.

Parameters vs Memory Memory가 활성화 크기에 의해 결정되는 경우가 많기 때문에 prarameters 개수가 반드시 학습 중 메모리 소비를 나타내는 것은 아니다. 따라서, 더 큰 activation을 가진 EfficieNet이 3.8배 적은 파라미터를 가지지만 2.3배 느린 잉이다. 따라서, 메모리 소비량과 지연시간이 스프트웨어 및 하드웨어 스택과 밀접하게 연결되어 있음을 강조한다.

7.2 Improving the Efficiency of EfficientNets

Section 6에서 말했던 image resolution이 성능을 저하시키는 것에 대한 분석이다. EfficientNet은 depth, width 그리고 resolution이 독립적으로 사용하여 sub-optimal에 도달한 것이다. 따라서, width와 depth를 바꾸지 않고 여러 resolution을 사용해 여러 version을 만들어 학습했다. RandAugement를 10: <=224 15: 224< R < 321 20: 320 > 로 사용했으며, 그림 5에서 re-scaled EfficientNets이 더 좋은 성능을 보임을 나타낸다.

7.3 Semi-Supervised Learning with ResNet-RS

ResNet-RS를 large scale semi-supervised learning setup에 적용하면 어떤가로 실험을 진행함. Noisy Student와 비슷하게 1.2M labeled ImageNet images와 130M pseudo-labeled images로 섞은 데이터셋으로 학습을 했다. 그렇게 한 결과는 밑의 표4에 나타나며, 성능은 비슷하며 속도에서 매우 큰 이점을 가진다.

7.4 Transfer Learning of ResNets-RS

최근 self-supervised learning algorithms이 transfer learning performance를 능가했다고 주장한다. 하지만, supervised learning에 비해 설정이 어렵다. SimCLR와 SimCLRv2와의 비교를 위해 실험을 진행했는데, 논문에서 제안하는 방법을 조금 바꿨다.

• Rand Augmentation, label smoothing, dropout, decreased weight decay, cosine lerning rate decay, 400 epoch
• No using stochatic depth or EMA
• No using ResNet-D and SE block

위의 제한을 걸어둔 것은 SimCLR: 긴 학습, data augmentation 그리고 temperature parameter for their contrastive loss와 architecture를 맞추기 위해서 이다.

밑의 표 5는 결과를 나타낸다.

보는 것처럼 ResNet이 더 좋은 성능을 보이며, 이는 self-supervised algorithms이 supervised보다 더 많은 universal representations을 가진다는 것에 반박할 수 있다.

7.5 Revised 3D ResNet Video Classification

나중에

8. Discussion

Why is it important to teas apart improvements coming from training methods vs architecures? (학습 방법과 구조를 구분하면 좋은 이유) 학습 방법이 네트워크 구조보다 task-specific하다. 즉, 더 좋은 학습 방법으로 새로운 구조를 쌓는 것이 더 일반적이라는 것이다.

How Should one compare different architectures? 학습 방법과 확장은 일반적으로 성능을 증가시키므로, 서로 다른 네트워크 구조를 비교할 때 두 측면 모두 제어하는것이 중요하다. 따라서, FLOPs와 parameters보다 latency와 memory consumption을 사용하는 것이 더 일반적일 것이다.

Do the improved training strategies transfer across tasks? domain과 dataset 크기에 따라 다르다. 여기서 사용된 많은 학습/정규화 방법은 large-scale pre-training에서는 사용되지 않는다. data augmentation 또한 작은 데이터셋 또는 큰 epochs에서 유용하며, 특정 augmentation 기법은 task의존적이다.

Do the scaling strategies transfer across tasks? section 6에서 보는 것과 같이 350 epoch에서는 depth가 10epoch에서는 width가 더 좋은 성능을 보였다. 즉, 최고 성능 scaling strategy는 학습 방법과 overfitting 유무에 따라 다르다. 저자들은 resolution을 늘리는 것에 대해서도 확신을 하지 못했으며 future work로 남겨둔다.

Are architectural changes useful? 당연히 좋지만, 학습 방법이나 scaling strategies가 더 큰 영향력을 가진다. 그 이유는 네트워크 변경은 너무 복잡하고 느려질 수 있기 때문이다. 나중에는 hardware 친화적인 네트워크 구조가 나오기를 기대한다.

How should one allocate a computational budget to produce the bset vision models? 먼저, 하드웨어 효과적으로 사용할수 이는 쉬운 네트워크부터 시작하여 점차 다른 resolution, depth, 그리고 width를 Pareto curve에 맞춰 적용해야한다. 이는 NAS와는 다른데, NAS는 너무 제한된 환경에서 네트워크 구조를 찾으며, RegNet은 단지 10 epoch만은 사용한다.

9. Conclusion

향상된 scaling 전략과 최신의 학습 방법으로 resNet 구조의 놀라운 duration을 보여주었다. 저자들은 자신들이 주장하는 바에 대해 더 많은 연구를 하기를 장려한다.

Designing Network design Spaces

I. Radosavovic R. P. Kosarahu R. Girshick K. He P. Dollar

Abstract

본 논문의 목표는 네트워크 설계에 대한 이해를 높히는 것이고 설정 전반에 걸쳐 일반화되는 설계 원칙을 발견하는 것이다. 개별적인 네트워크 인스턴스 설계에 초점을 맞추지 않고 네트워크 모집단을 매개 변수화하는 네트워크 설계 공간을 설계한다. 기존의 네트워크 디자인과 비슷하지만 디자인 space level이 더 높다. 본 논문은 네트워크 디자인의 구조적인 측면을 연구했으며, RegNet이라 불리는 단순하고 규칙적인 네트워크로 구성된 low-dimension 설계 공간에 도달했다고 한다. RegNet 매개변수화의 중심

insight는 놀랍게도 단순한데: 좋은 네트워크의 widths와 depths는 quantized linear function으로 설명될 수 있다. RegNet의 디자인 공간을 분석했는데, 최근 네트워크 디자인 실정과는 다름을 나타낸다. RegNet의 디자인 공간은 단순하고 flop 여역에서 매우 좋은 성능을 보이는 빠른 네트워크이다. RegNet은 EfficientNet 모델보다 GPU에서 5배나 더 빠르다.

1.Introduction

LeNet~ResNet까지는 효과적이면서 잘 알려지 네트워크 디자인이다. 위의 네트워크들은 convolution, network 그리고 데이터 크기, depth, residuals 등 각각이 중요하다는 것으 알려준다. 이것은 실질적인 네트워크 예시이며 디자인 원칙이다.

직접 네트워크를 설계하는 것이 큰 발전을 이뤄았지만, 선택의 수가 증가함에 따라 잘 최적화된 네트워크를 수동을 찾는 것은 어렵다. 따라서, NAS 라고 불리는 고정된 search space에서 가능한 좋은 네트워크를 찾아주는 기술이다.

NAS는 특정 설정에서 단일 네트워크 인스턴스만을 찾는 한계가 존재하며, 본 논문은 일반화를기반으로 하는 매우 단순한 네트워크를 찾는 것에 집중한다.

따라서, 본 논문은 수동의 디자인과 NAS의 이점을 조합한 새로운 네트워크 디자인 파라다임을 제시한다. 즉, 매개변수화 시킨 네트워크의 모집단인 디자인 공간들을 디자인한다. (여기서 디자인 공간은 탐색 공간이 아니다. 네트워크 인스턴스를 찾는 것이 아닌 말 그대로 공간을 디자인하는 것이다.)

전체적인 과정은 수동 디자인 방법과 유사한데, 모집단 수준으로 올리고 네트워크 디자인 공간들을 분산 평가를 통해 이끌어낸다.

먼저, VGG, ResNet, 그리고 ResNeXt와 같은 네트워크 구조를 찾았으며, 상대적으로 자유로운 디자인 공간을 가지는 AnyNet을 만들었고, 단순한 "regular" 네트워크로 이뤄진 저차원 디자인 공간을 발견했다. stage widths와 depths를 양자화 선형 함수로 결정할 수 있는 공간이다. AnyNet과 비교해 더 단순하고, 해석하기 쉽고, 좋은 모델들에 더 많이 집중할 수 있다.

RegNet의 디자인 공간은 적은 계산, 적은 epoch을 가진다. 더 쉽게 해석가능하고 우리가 생각한 방식과 이어진다. 또한, 기존의 일반적인 생각과 다르게, bottleneck 또는 inverted bottleneck을 사용하지 않고도 20 block 가까이 에서도 안정적임을 보인다.

RegNet은 모바일 환경에서 더 효과적이며, ResNe(X)t보다 더 좋은 성능을 보인다. 그리고 활성화 함수 횟수가 GPU와 같은 가속기의 런타임에 큰 영향을 미칠 수 있으므로 고정된 활성화함수에 대한 개선된 점을 강조한다. 또한, EfficientNet보다 5배나 더 빠르며, 일반화 성능도 높다.

네트워크 구조는 고려할 수 있는 디자인 공간 디자인의 가장 단순한 형태라고 할 수 있으며, 더 풍부한 설계 공간을 설계하는데 집중하면, 더 나은 네트워크로 이어질 수 있음을 나타낸다.

2. Related Work

Manual network design AlexNet부터 이어져온 manual network design은 많은 발전을 이뤄왔다. 이와 비슷하게 본 논문도 새로운 디자인 원칙을 발견했으며, manual design과 비슷하며 단지 디자인 공간 수준에서 실행되는 것이 차이점이다.

Automated network design 최근에는 NAS를 통해 효과적인 네트워크를 찾는데 집중한다. 본 논문은 search space를 디자인하는 방향으로 연구를 했으며, 2가지의 가정이 깔려있다. 1) 더 좋은 디자인 공간은 효과적으로 NAS의 search algorithm을 개선시킬 것. 2) 디자인 공간이 풍부해지면 더 좋은 모델을 찾을 수 있을 것.

Network scaling. 보통 네트워크를 만들 때는 특정 영역(flops, compare, etc)에서 최고의 성능을 내는 것으로 찾기 때문에, 다른 영역에서 사용하기에는 좋지않다. 따라서, 본 논문은, 일반적인 디자인 원칙을 발견함에 동시에 어떤 목표 영역에서도 최적화된 네트워크로 효과적으로 튜닝을 할 수있는 네트워크를 찾는다.

Comparing networks. 네트워크 디자인 공간들의 수는 거대하기 때문에, 뛰어난 comparison metric은 필수적이다. 최근에는 새플림 된 네트워크 모집단을 비교하고 분석하는 방법론이 존재하는데, 본 논문의 목표와 일치하며, 효과적인 방법을 제안한다.

Parameterization. 최종 양자화 선형 파라미터화는 이전 논문들과 비슷하지만, 다른 점이 2가지 있다. 1) 설계 선택을 정의하는 실증적 연구를 제공함. 2) 이전에 이해하지 못했던 구조 설계 선택에 대한 insight를 제공함.

3. Design Space Design

특정 설정에서 단일의 최고 모델을 찾거나 디자인하는 것보다는, 모델들의 모집단의 행동을 연구하는 것이다. 일반적인 디자인 원칙을 발견하고 이것을 모델의 모집단에 적용하는 것이다.

Radosavovic et al. [21][21]의 디자인 공간 개념을 사용하는데, 디자인 공간으로부터 모델들의 샘플링하고, 모델 분포를 생성하며, 그리고 고전 통계방법으로 이러한 디자인 공간을 분석할 수 있다는 것이다.

본 논문은 자유로운 디자인 스페이스에서 계속해서 단순한 버전의 initial network을 디자인하는 design space design을 제안한다. 입력은 초기의 디자인 공간이며 출력은 더 단순하거나 좋은 성능을 가진 모델들의 모집단을 가지는 디자인 원칙인 재정의된 디자인 공간이다.

본 논문에서 제안하는 RegNet의 디자인 공간은 다음과 같다. 1) 허용하는한 네트워크 구성의 차원과 유형 측면에서 단순화 2) 최고 성능 모델들의 더 높은 집중이 포함되어있으며, 3) 분석 및 해석이 더 용이해야한다.

3.1 Tools for Design Space Design

본 논문은 디자인 공간을 평가하기 위해 [21][21]의 방법을 사용하는데, 해당 설계 공간에서 모델 세트를 샘플링하고 모델 오류 분포 결과를 특성화하여 설계 공간의 품질을 정량화한다. 이것은 분포를 비교하는 것이 더 강인하며 search algorithms을 사용하는 것보다 더 유익하다.

모델의 분산을 얻기위해 디자인 공간에서 n개의 모델을 샘플링하고 학습한다. 효율성을 위해 400M FLOPs와 10 epochs만을 사용한다. n이 100일 때, 모델들 모두를 학습하는 것과 ResNet-50을 학습하는 것과 같은 FLOPs를 가진다. (ImageNet에서 학습한 결과)

[21][21]의 디자인 공간의 퀄리티를 분석하기위 empirical distribution function (EDF)를 사용한다.

$e_i$는 모델의 에러이며 $e$는 threshold이다.

밑의 그림 2의 좌측은 $n=500$에서 AnyNetX 디자인 공간으로부터 샘플링한 모델들의 EDF 이다. 훈련된 모델의 모집단이 주어지면 다양한 네트워크 속성과 네트워크 오류를 시각화하고 분석할 수 있다.

여기서, empirical bootstrap를 통해 최고 모델이 속하는 범위를 추정할 수 있다.

즉, 이렇게 요약할 수 있다. 1) 디자인 공간으로부터 n개의 모델을 샘플링하고 학습하여 모델의 분포를 얻는다. 2) EDF를 사용해 디자인 공간의 퀄리티를 계산하고 시각화한다. 3) 디자인 공간의 속성을 보고 empirical bootstrap을 통해 insight를 얻는다. 4) 이것으로 다시 디자인 공간을 재정의하여 더 나은 디자인 공간을 만든다.

3.2 The AnyNet Design Space

이 section에서는 표준이며 고정된 네트워크르 블럭을 가정한 네트워크의 구조를 탐구하는 것이다. 즉, 블럭의 수, 블럭의 너비 그리고 블럭의 다른 매개변수들에 대한 탐구다. 이러한 것들은 계산량, 매개변수 그리고 메모리의 분포를 결정하는 동시에 정확도와 효율성을 결정한다.

AnyNet의 디자인 공간은 간단하면서 쉬운데, 그림 3의 a와 같이 입력단의 stem, 그 뒤에 body 그리고 class를 예측하는 head 부분으로 나눠져있다. 여기서 stem과 head를 최대한 고정시키고 네트워크의 body를 변경하여 계산량과 정확도를 결정한다.

body는 총 4개의 stages로 구성되어 있으며, 계속해서 resolution을 줄여간다. (그림 3의 b) 각 stage는 개별적인 block들을 가지며, 각각의 stage는 block의 갯수 ($d_i$), block의 너비 ($w_i$), 그리고 block 매개변수를 가진다. 이러한 AnyNet의 구조는 매우 방대하다.

그림 4에서 볼 수 있듯이 대부분의 실험에서는 residual bottleneck blcok을 사용하며, 이것을 x block 이라고 지칭한다. 그리고 이러한 block으로 이뤄진 네트워크를 AnyNetX라고 하며, 네트워크 구조가 최적화 되었을 때, 놀랍운 효율성을 보인다.

AnyNetX의 디자인 공간은 총 16단계로 정해지는데 4개의 stage와 각 stage에서 4개의 매개변수를 가진다. blocks의 수 ($d_i$), block의 너비 ($w_i$), bottleneck ratio ($b_i$), 그리고 group width ($g_i$)이다. $d_i \leq16$인 log-uniform sampling, $w_i \leq 1024$인 8의 배수, $b_i \in {1,2,4}$, $g_i \in {1,2,...,32}$ 이다. $n=500$, epoch 은 10, 그리고 목표 계산량은 300MF~400MF이다.

총 $10^18$의 가능성이 나오며 이것이 AnyNetX의 디자인 공간이다. ~$10^18$의 최고성능 모델을 찾는 것이 아닌 일반적인 디자인 원칙을 찾는데 집중했으며 디자인 공간을 이해하고 재정의 하는데 도움이 된다. 그리고 4가지의 접근법을 사용해 AnyNetX를 총5가지로 나눴다.

AnyNey$X_A$ 초기의 AnyNetX의 디자인 공간이다.

AnyNet$X_B$ 여기서 제한하는 부분은 bottleneck ratio를 공유하는 것이다. 즉, 모든 stage에서 bottleneck ratio $b_i = b$로 고정한다. 똑같이 500개의 모델을 만들어 AnyNet$X_A$와 비교했으며, 그림 5의 좌측은 결과이다. 이것으로 보아 bottlenck ratio는 그렇게 큰 차이를 못내는 것 같으며 그림 5의 우측은 b에 따른 결과를 보여준다.

AnyNet$X_C$ 여기서는 AnyNet$X_B$에서 group convolution을 공유했다. 성능 변화는 거의 없어 보이며 그림 5의 중앙을 보면 알 수 있다.

AnyNet$X_D$ 여기서는 AnyNet$X_C$의 좋은 네트워크와 안좋은 네트워크를 탐구했으며, 그림 6에서 볼 수 있다. 결과적으로 widths가 증가할 수록 성능도 증가하는 패턴을 발견했다. 따라서, $w_{i+1} \geq w_i$라는 디자인 원칙을 발견했다. 그림 7에서 확연하게 알 수 있다.

AnyNet$X_E$ 여기서는 stage depths $d_i$를 width와 같이 형성했다. 즉, $d_{i+1} \geq d_i$이다. 그림 7에서 볼 수 있으며, $w_i$와 $d_i$는 각각 4!만큼 줄어들었다. 따라서, $O(10^7)$만큼 가진다. <-> $O(10^18)$

3.3 The RegNet Design Space

그림 8의 상단좌측은 AnyNet$X_E$의 최고 20개의 모델을 보여준다. 또한, grady curves는 각각 모델의 편차를 보여주는데, 패턴이 나타난다. ($w_j=48\cdot(j+1)\ and\ 0 \leq j \leq 20$)이다. 놀랍게도 이 사소한 linear fit은 상위 모델에 대한 네트워크 너비 증가의 모집단 추세를 설명하는 것 같다. 하지만, linear fit는 각 블럭마다 다른 width를 할당하는 것처럼 보일 수 있다.

이러한 패턴을 개별적인 모델들에 적용하기위 piecewise constant function을 양자화하는 전략을 선택했다. 즉, 각 block의 너비들을 linear parameterization로 할당한다

$d$: depth, $w_0 >0$: initial width, $w_\alpha >0$: slop, 그리고 각 block $j<d$에서 다른 너비인 $u_j$를 가진다.

$u_j$를 양자화 하기위해서 추가적인 매개변수인 $w_m >0$을 소개한다. 먼저, $u_j$로부터 각 블럭 j 에서 $s_j$를 계산한다.

그 후에, $u_j$를 양자화 하기위해 $s_j$를 반올림하고 블럭당 너비인 $w_j$를 양자화하여 계산한다.

block당 width인 $w_j$를 stage당 width로 확장하고 $w_i=w_0\cdot w_m^i$와 같이 된다. 그리고 블럭의 갯수인 $d_i=\sum_j1[\left [s_j \right] = i].$가 된다. 4단계 네트워크 만 고려할 때 다른 수의 stage를 발생시키는 매개 변수 조합을 무시한다.

AnyNetX에 위의 매개변수화를 적용해서 테스트를 진행했으며, d로 네트워크 깊이를 설정하고 grid search를 통해 $w_0,\ w_\alpha$를 찾았다. 그 후 $w_m$은 관측된 블록당 너비로 예측된 $e_{fit}$라고 불리는 평균 로그 비율을 최소화한다. 그림 8의 상단 우측에서 dashed curves는 양자화 linear fits가 최고 모델 (solid curves)와 유사하다.

fitting error인 $e_{fit}$와 네트워크 에러를 살펴보기위해 그림 8의 하단을 보면 된다. 각 디자인 공간에서 최고 모델이 좋은 linear fits를 가짐에 주목했으며, 실제로 각각의 디자인 공간 안에서 최고 모델은 $e_{fit}$의 좁은 영역 안에 포함된다. 그리고 평균에도 주목했는데, $X_c$에서 $X_E$까지 감에 따라 $e_{fit}$가 개선되며 이것은 $w_i$와 $d_i$가 증가하면 성능도 좋아짐을 나타낸다.

더욱더 디자인 공간을 제한했으며, 6개의 파라미터들인 $d,\ w_0,\ w_m, w_\alpha,\ b,\ g$로 구성된다. 각각으로 위의 2~4 수식을 통해 block width와 block depth가 정해지고 이것은 RegNet이라고 부른다. $d<64,\ w_0,w_\alpha <256,\ 1.5 \leq w_m \leq 3$ and $b$ and $g$는 전의 AnyNet$X_E$와 같다.

그림 9의 좌측을 보면 AnyNetX보다 RegNetX가 훨씬 더 좋은 성능을 보인다. 또한 2가지의 단순화를 시켰는데, 그림 9의 중앙을 보면 1) $W_m=2$(stage마다 width는 2배)로 성능을 증가시킴 2) $w_0=w_\alpha$는 수식 2인 선형 매개변수화를 단순하게 만들며 성능 또한 좋아진다. 하지만, 다양성을 위해 이와같은 방법은 사용x 그리고 그림 9의 우측은 RegNetX의 random search 효율성을 보여준다.

표1은 AnyNetX와 RegNetX의 디자인 공간 크기에 대한 표이며, 약 $10^10$만큼 줄었지만 여전히 RegNet은 다양성을 가지고 있다고 주장한다.

3.4 Design Space Generalization

본논문에서 RegNet을 디자인 했지만, 더 일반화된 설정을 발견했다.

일반화를 위해서 먼저 AnyNet을 더 많은 flops, 더 많은 epochs 그리고 5-stage networks로 구성해서 성능을 테스트 했다. 여기서도 RegNet이 성능이 더 뛰어 났으며, overfitting의 징조를 보지 못했다. 이것은 아직도 RegNet이 더 많은 stages 에서도 일반화될 수도 있다는 것이다.

4. Analyzing the RegNetX Design space

RegNetX의 디자인 공간을 분석하고 공통적으로 deep network 디자인에서 많이 선택하는 것을 조사했다. 여기서는 $N=100,\ epoch=25,\ learning\ rate=0.1$로 사용했다.

RegNet trends.

1) depth: 약 20 blocks(60 layers)에서 최적화된다. -> 깊이가 늘어날 수록 성능 증가한다는 일반적인 이론과 다름 2) bottleneck ratio: 1.0에서 최적화된다. -> bottleneck 구조가 좋다는 일반적인 이론과 다름 3) width multiplier: 2.5에서 최적화된다. -> 일반적인 이론은 2배를 보통 한다. 4) 남은 매개변수들: 복잡해질수록 성능이 증가한다.

Complexity analysis.

모든 conv layers의 출력 텐서 크기를 뜻하는 activations에 대한 탐구이다. 그림 12의 상단을보면 actiavtions은 GPUs, TPUs와 같은 메모리가 제한된 하드웨어 가속이의 실행시간에 크게 영향을 준다. 그림 12의 하단에서 특히 모집단의 최고 모델을 보면, activaations는 FLOPs의 제곱근을 증가시키며, 매개변수들도 선형적으로 증가시키며, 실행시간은 선형과 제곱근의 조합으로 설명될 수 있다.

RegNetX constrained 위의 결과들을 종합해 새로운 디자인 공간을 정의했다. 1) 그림 11의 상단을 참고하여 $b=1,\ d \leq 40,\ and\ w_m >2$로 설정함. 2) 그림 12 하단을 참고해 매개변수와 activation을 제한함. 3) 따라서, 빠르고, 적은 매개변수와 적은 메모리를 가지는 모델을 만들었으며, 그림 13에서 확인할 수 있다.

보는 것과 같이 모든 FLOPs에서 더 좋은 성능을 보인다.

Alternate design choices.

최근 모바일 네트워크에서 inverted bottleneck (b<1)와 depthwise conv(g=1)을 강조했는데, 이와 같은 방법은 그림 14 좌측을 보면 성능 저하를 가져오는 것을 확인할 수 있다. 그리고 input image를 증가시키면 도움이 된다고는 하지만, regNetx는 $224\times224$로 고정하는 것이 제일 좋은 성능을 보인다.

SE. 자중 사용되는 Squeeze-and-Excitation (SE) op를 추가해 RegNetY로 부르며 그림 14의 우측과 같이 좋은 성능을 보인다.

5. Comparison to Existing Networks.

ImageNet에서 비교를 위해 RegNet 매개 변수의 25가지로 임의 설정에서 최상의 모델을 선택하고 상위 모델에 대해 100epoch으로 5번 재훈련한다.

그림 15와 그림 16은 각각 RegNetX와 RegNetY의 성능을 보여준다. 여기서 흥미로운 패턴을 발견했는데, 상위 플롭 모델은 3 stage에 많은 수의 블럭이 있고 마지막 단계에 적은 수의 블럭을 가지는데 이것은 ResNet과 유사하다.

본 논문의 목표는 공평한 비교와 쉽고 재생산할 수 있는 baselines를 제공하는 것이다. 따라서, 특별한 학습 구성이나 정규화를 사용하지 않았다.

5.1 SOTA Comparision: Mobile Regime

모바일 영역은 보통 600MF보다 작은 영역을 뜻하는데 표2에서 보는 것과 같이 RegNet이 더 좋은 성능을 보인다.

또한, 비교된 네트워크 구조는 더 긴 학습 시간과 많은 정규화를 사용했기 때문에, RegNet이 더 좋은 성능을 가져올 수 있다고 생각한다.

5.2 Standard Baselines comparison: ResNe(X)t

ResNet과 ResNeXt에 대한 비교이며, 모든 학습 설정은 ResNet과 ResNeXt를 따랐다. 그림 17과 표 3을 보는 것처럼 매우 좋은 성능을 보인다.

activations으로 따로 구별한 이유는 activations의 수가 GPU와 같은 가속기의 실행시간에 영향을 주기 때문이다. 따라서, RegNetX는 적은 실행시간을 가지므로 효과적이다.

5.3 SOTA Comparison: Full Regime

EfficientNet과의 비교이다. EfficientNet을 재구현하였으며, 본 논문 저자들이 정한 학습 설정인 100 epoch과 정규화 비사용을 사용함. 오직 learning rate와 weight decay를 사용했으며, RegNet과 같은 설정이다. 결과는 그림 18과 표 4에서 볼 수 있으며, 적은 flops에서는 EfficientNet이 더 좋지만 큰 flops에서는 RegNetY이 더 좋은 성능을 가진다. 또한, EfficientNet이 더 많은 activations을 가지는 것으로 보이는데, 이것은 추론 시간을 증가시켜 RegNetX-8000이 EfficientNet-B5보다 약 5배 빠르다.

6. Conclusion

새로운 네트워크 디자인 표준을 제시했으며, 네트워크 디자인 공간을 디자인 하는 것이 유망있는 기술이면 좋겠다.

VarGFaceNet: An Efficient Variable Group convolutional Neural Network for Lightweight Face Recognition

M. Yan M. Zhao Z. Xu Q. Zhang G. Wang Z. Su

Abstract

본 저자들은 VarGFaceNet이라고 불리는 효율적인 variable group CNN을 제안한다. parameter와 cost를 줄이는데 집중을 했다. 특히, 특정한 설정이 필요한데, 네트워크의 입력단인 head와 fully-connected layer에서 특정 embedding stting이 필요하다. 저자들은 재귀적인 knowledge distillation을 사용했으며, teacher와 student 사이의 차이를 없애는 방향으로 접근하였다. 2019년 LFR deepglintlight에서 1등을 했다고 한다. github: https://github.com/zma-c137/VarGFaceNet

1. Introduction

얼굴 인식 분야에서 계산량을 줄이는 많은 논문들이 있지만, 여전히 제한적이다. SqueezeNet, MobileNet, ShuffleNet과 같이 $1\times1$ convolution을 사용해 사용량을 줄인 것들이 있다. MobileNet v1의 경우 depthwise separable convolution을 사용했으며, 그에 기초해 MobileNet v2는 반전된 bottlenect 구조로 네트워크의 분별능력을 강화했다. ShuffleNet 종류는 pointwise group convolution과 channel shuffle operation을 통해 계산량을 줄였다. VarGNet은 variable group convolution을 통해 블럭당 불균등한 계산량을 해결했다. 특히, 같은 kernel 크기에서 depthwise convolution보다 더 많이 수용할 수 있다. 그러나 VarGNet은 얼굴인식에는 적합하지않는데, 네트워크 시작단에서 공간영역을 반으로 줄이는 특성 때문이다. 얼굴 인식은 얼굴 이미지의 자세한 정보가 중요하다. 또한, average pooling layer가 마지막 conv와 fc layer 사이에만 있어, 충분한 분별 정보를 추출할 수 없다.

VarGNet을 기반으로 제안하는 VarGFaceNet이다. VarGNet과는 다르게 추가한 부분들이 있다. 1) SE block과 PReLU를 추가함 2) 더 많은 정보를 보존하기위해 네트워크 시작 부분의 downsample process 제거 3) embedding 때, fclayer 전에 $1 \times 1 \times 512$에 variable group convolution 적용.

네트워크의 해석 능력을 강화시키기위해 학습하는 동안 Knowledge distillation을 적용했다. 더 작고 효율적인 네트워크를 위해 pruning, quantization 등이 있는데, knowledge distillation의 경우 모델 변경이 자유로워 선택했다. Hinton 11은 knowldege distillation 개념에 대해서 소개했으며, FitNet은 feature distillation 아이디어를 채택하여 student network가 teacher network의 hidden feature를 따라할 수 있도록 했다. 그 후로, transferring the fature activation map 10과 activation-based and gradient-based Attention Maps 25 이 시도되었다.최근에는 ShrinkTeaNet 6은 angular distillation loss로 teacher model의 angular information에 집중했다. 게다가, teacher model과 student model 사이의 차이에 의해 발생하는 optimization의 복잡성을 해결하기위해 다음 세대를 위해 pretrained model을 한 세대에 student를 학습하는데 사용하였다.

본 논문은 LFR challenge에서 1등을 달성했으며, 좋은 성능을 보였다.

Contribution

• VarGNet에서 다른 head setting과 새로운 embedding block을 제안했다. 새로운 embedding block은 처음에 $1 \times 1$ convolution을 통해 1024 channel로 확장하고 variable group conv와 pointwise conv를 적용했다.
• generalization을 위해 recursive knowledge distillation을 사용함
• variable group convolution의 효율성과 angular distillation loss와의 동일성을 분석함.

2. Approach

2.1 Variable Group convolution

Group convolution은 AlexNet부터 이어져온 기술이다. ResNext에서는 group convolution의 개수에 대해서 설명했으며, MobileNet들은 이것으로 depthwise separable convolution을 만들었다. 하지만, 계산량 대부분 (95%)을 $1\times1$에서 사용된다. 따라서, 이런 차이는 embedding 방법에는 적합하지 않는다. 따라서, VarGNet은 channel를 상수 $n_i$로 나눈 $S$를 사용한다. VarGNet의 계산량은 다음과 같다.

입력층의 $h_i \times w_i \times c_i$이며 출력층의 $h_i \times w_i \times c_{i+1}$ 이다. $k$는 kernel의 크기이다. 만약, MobileNet의 depthwise separable convolution 대신에 group convolution이 쓰인다면 pointwise convolution 같이 나온다.

variable group convolution과 pointwise convolution 사이의 계산량 비율은 $\frac{k^2S}{c_{i+2}}$이며 depthwise convolution과 pointwise convolution 사이의 비율은 $\frac{k^2}{c_{i+2}}$ 이다. 실제로 $c_{i+2}\gg k^2,\ S>1,$이므로 따라서, $\frac{k^2S}{c_{i+2}} > \frac{k^2}{c_{i+2}}$ 이다. 따라서, depthwise separable convolution 대신 pointwise convolution의 하단에 variable group convolution을 사용하면 블록 내에서 더 계산적으로 균형을 이룬다. 게다가, $S>1$은 더 많은 MAdds와 더 큰 네트워크 수용력을 나타내며, 더 많은 정보를 추출할 수 있음을 나타낸다.

2.2 Blocks of Variable Group Network

VarGNet은 normal block에서 입력 채널과 출력 채널의 수를 같게 했지만, 시작부분 block에서는 일반화 능력을 유지하기위해 C 채널 수를 2C 채널 수로 확장했다. 위의 그림 (a)과 (b)와 같이 구조를 쌓았으며, 구별능력 향상을 위해 normal block에 SE block을 추가하고 ReLU 대신 PReLU를 사용했다.

2.3 Lightweight Network for Face Recognition

2.3.1 Head setting

face recognition은 규모가 큰 문제이다. lightweight network를 유지하기 위해 $3\times3$ Conv에 stride를 1로 설정해 사용했으며 (VarGNet에 비해), 시작부분에서 downsampling이 아닌 그대로 사용했다. 그림 1의 (c)에서 확인할 수 있다.

2.3.2 Embedding setting

얼굴의 embedding을 얻기 위해서 많은 논문들이 마지막 convolution 뒤에 fc layer을 붙이는데 상대적으로 매우 큰 계산량을 차지한다. 예를들어 ReNet 100의 경우 49M에서 12.25M을 차지한다.

본 논문에서는 variable group convolution을 통해 fc layer 전에 $1\times1\times512$ feature map으로 줄어들게하였으며, fc layer에서 단지 1M만 사용한다. (그림 1의 (d)에서 확인 가능) 하지만, 이렇게 하면 feature tensor가 제한될 수 있어 마지막 conv layer 전에 늘리고 줄이는 방식을 통해 필수적인 정보는 감소되는 것을 방지하도록 했다.

1) $1\times1$ convolution을 통해 $7\times7\times320$에서 $7\times7\times1024$로 확장.

2) $7\times7$ variable group convolution을 통해 $1\times1\times7$로 줄어들게 함.

3) pointwise convolution을 통해 $1\times1\times512$로 만든다.

이렇게 새로운 embedding은 기존의 embedding인 30M에 비해 5.78M의 계산량을 가진다.

2.3.3 Overall architecture

약 20M 메모리와 1G의 FLOPs를 사용한다. 전체적인 구조는 표 1에서 확인할 수 있다.

2.4. Angular Distillation Loss

Knowledge distillation은 큰 네트워크에서 작은 네트워크로 해석 능력을 전달할 수 있다. scores/logits 또는 embeddings/feature magnitude에 L2/cross entropy를 사용한다. 하지만, 이런 것은 제한된 정보를 주거나 over-regularized 될 수 있다. 따라서, angular distillation loss라는 것을 사용해 유용한 정보를 추출하고 over-regularization을 피할 수 있다. 밑의 식은 angular knowledge distillation 이다. $F_t^i$는 i번째 teatcher, $F_s^i$는 i번째 student이다.

본 논문에서는 위의 angular knowledge distillation을 구현의 편의성을 위해 변형하여 다음과 같이 사용한다.

또한 arcface를 차용하여 angular information에 더 지 ㅂ중한다.

따라서, 최종 학습시킬 objective function은 다음과 같다.

본 논문에서는 실험적으로 $\alpha=7$을 사용한다.

2.5 Recursive Knowledge Distillation

단 한 세대의 Knowledge distillation은 큰 모델과 작은 모델 사이의 간극을 때때로 매꿀 수 없을 때도 있다. 따라서, student network의 구별 능력과 일반화 능력을 향상시키기 위해 recursive knowledge distllation을 사용한다. 그리고, teacher network를 매 새대 같은 것을 사용해 지도되는 내용이 불변하도록 한다. Recursive knowldege distillation을 통해 얻는 이점은 다음과 같다.

1. teacher로 부터 곧바로 지도를 받아 좋은 초기화를 제공할 수 있다.
2. classification loss와 angular information 사이의 충돌을 다음 세대를 통해 해결할 수 있다.

3. Experiments

1) y2 network (deeper mobilefacenet)과 비교 2) 다른 teacher model들과 비교 3) LFR2019 Challenge에 적용한 성능

3.1 Datasets and Evaluation Metric

먼저 Training에는 LFR2019에서 제공하는 MSIM으로 모든 학습을 진행했으며, 모든 어굴 이미지는 RetinaFace로 $112\times112$로 재조정해서 사용했다. Testing에서는 Trillionpairs dataset을 사용했다. 위의 데이터 셋은 ELFW, DELFW를 포함하는 데이터셋이다. 모든 테스트 얼굴 이미지는 preprocess와 resize를 했다. 마지막으로 Evaluation은 LFW, CFP-FP 그리고 AgeDB-30을 사용했다. 또한, TPR@FPR=1e-8로 evaluation metric을 사용했다.

3.2 VarGFaceNt rain from scratch

Validation set에서 mobilefacenet (y2)와 비교한다. 표 2에서 확인할 수 있으며, 전체적으로 본 저자들이 만든 네트워크의 성능이 더 높게 나온다. 직관적으로 2가지의 나은 성능을 볼 수 있다.

1. y2에 비해 더 많은 파라미터들을 포함하고 있으며, 마지막 conv layer에서 256에 비해 320 채널 수를 가진다.
2. y2의 경우 256에서 512로 확장하지만, 본 논문의 네트워크는 320에서 1024로 확장한다. 따라서 더 많은 정보를 가진다.

3.3 VarGFaceNet guided by ResNet

angular distillation loss를 사용해 knowledge distillation을 했다. teacher model로는 SE block이 포함된 ResNet 100을 사용했다. 결과는 표 3에서 확인할 수 있다. 표의 결과에 따라 VarGFaceNet이 더 작은 네트워크 이지만, teacher model을 따라잡을 수 있음을 알 수 있다.

VarGFaceNet과 VarGNet을 비교했다. 여기서 VarGNet은 VarGFaceNet과 같은 head 설정을 했으며, 결과적으로 VarGFaceNet이 더 좋은 성능을 보인다. 즉, VarGFaceNet의 embedding setting이 더 적합하는 것을 알 수 있다.

3.4 Recursive Knowledge Distillation

VarGFaceNet을 recursive Knowledge Distillation으로 validation set에 사용한 결과이다. 표 5에서 확인할 수 있으며, LFW와 CFPFP는 0.1%의 상승을, deepglintlight는 0.4%의 상승을 확인할 수 있다. 저자들은 더 많은 generation을 통하면 성능을 더 증가할 것으로 생각한다.

4. Conclusion

본 VarGFaceNet으로 효율성과 성능 사이의 trade-off를 더 좋게 할 수 있음을 알게되었다. head setting과 embedding setting으로 information을 보전할 수 있으며, angular distillation loss와 recursive knowledge distillation을 통해 해석능령이 상승한 가벼운 네트워크를 만들 수 있었다.

Dynamic Feature Learning for Partial Face Recognition

L. He H. Li Q. Zhang Z. sun

Abstract

Partial face Recognition (PFR)은 CCTV나 모바일 환경같은 자유로운 환경에서 매운 중요한 task이다. 본 논문은 Fully Convolutional Network (FCN)과 Dynamic Feature Matching (DFM)을 조합해 PFR문제를 해결한다. sliding loss롤 FCN을 최적화 하며 intra-variantion을 줄인다.

1. Introduction

full 또는 frontal images face recognition은 쉽게 해결할 수 있는 문제이다. 하지만 , PFR은 전통적인 face recognition approaches로는 해결하기 힘든 문제들이다. 그림1과 같이 모자, 마스트 또는 스카프를 착용하거나 사람이나 건물에 가려져서 인식하기 힘들다.

존재하는 face recognition algorithm들은 고정된 입력 사이즈를 사용한다. 하지만, MRCNN 10은 얼굴과 부분 얼굴로 구역을 나눠서 feature을 추출하고 인식에 사용했다. 하지만, 중복되는 구역을 보는 계산량의 문제가 있는데, 이것은 Sliding window Matching (SWM 43)을 사용하면 줄일 수 있다. 여전히 sliding window는 필연적으로 같은 구역을 반복적으로 탐색하기 때문에 효율이 좋다고 할 수는 없다.

Dynamic Feature Matching (DFM)으로 좋은 효율성과 모호한 크기의 얼굴 이미지를 다룰 수 있다. 밑의 그림 2는 DFM의 구조에 대한 것이다.

먼저, FCN으로 spatial feature map을 galley와 probe로 부터 뽑아낸다. 추출된 feature map은 VGGFace에 사용된다. 마지막 pooling layer은 입력된 face의 크기에 상관없이 똑같은 feature extractor가 사용된다. 그 다음에, gallery feature map은 sub-feature map으로 분해된다. 마지막으로 Sparse Representation Classification (SRC)에 의해서 probe feature map과 gallery sub-feature map과의 유사도를 구한다. DFM은 MR-CNN보다 20배는 빠르다고 하며, 논문에서 제안하는 sliding loss는 추출된 feature map과 anchor의 유사도를 계산할 수 있다고 한다.

Contribution:

1. FCN과 SRC를 조합한 DFM
2. 전체적인 얼굴 뿐만 아니라 부분적인 얼굴도 인식가능한 DFM
3. 더 많은 deep feature를 학습할 수 있는 sliding loss

2. Related Work

2.1 Deep Neural Networks.

CNN은 image classification, object detection 그리고 semantic segmentation을 해결할 수 있다. DeepFace 35 를 시작으로 VGGFace 26, Light CNN 39, FaceNet 32 그리고 SphereFace 16이 차례대로 등장했다. 게다가 최근에는 Spatial pyramid pooling (SPP) 8이 등장했는데, 모호한 크기의 인풋을 고정된 길이의 representation을 FCN에 제공할 수 있다.

2.2 Sparse Representation classification.

얼굴인식에 SRC를 사용한 유명한 논문은 38이며, 42, 40 등도 있다.

2.3 Partial Face Recognition.

Hu 11은 alignment 없이 SIFT descriptor representation이 가능한 방법을 제안했으며 instance-to-class (I2C)를 계산하였다. Liao 15는 alignment-free 접근 법인 multiple keypoints descriptor SRC (MKD-SRC)를 제안하였다. 본 방법은 keypoint들 사이에 변하지않는 것이 있으므로 그것을 특징으로 구별한다. Weng 37은 Robust Point Set Matching (RPSM) 방법을 사용해 SURF descriptor 그리고 LBP histogram을 적용하였다. region-based model들도 해결법으로 적용할 수 있다. 눈, 코, 얼굴의 반 그리고 눈 주위에 대한 정보를 사용하였다. 제일 최근에는 He 10 Multi-Scale Region-based CNNs (MRCNN)이 있다. 하지만 얼굴 구성과 pre-alignment가 필요하다. 따라서, 본 논문에선는 alignment-free PFR 알고리즘인 DFM을 소개하며 높은 정확도와 높은 효율성을 보인다.

3. Out Approach

3.1 Fully Convolutional Network

convolutional layer은 sliding-window 방법과 spatial 출력들을 만들어낸다. fully-connected layer는 고정된 차원 특징과 공간 좌표를 없애버린다. 따라서, 고정된 길이를 가져오는 fully-connected layer은 필요가 없다.
밑의 표1을 보면 VGGFace의 구조인데, fully-connected layer가 없다. 그 이유는 다양한 입력 사이즈에 대한 출력이 필요하며 더 견고한 feature를 뽑는데 필요가 없기 때문이다. 이처럼 모든 convolutional layer로 이루어진 구조를 Fully-convolutional network (FCN) 이라고 명명한다. FCN은 입력 크기의 제한 없이 서로 맞는 크기의 spatial feature map들을 뽑아낼 수 있다.

3.2 Dynamic Feature Matching

해당 섹션에서는 DFM에 대한 설명을 하는데, prob와 gallery에 대한 설명부터 한다.
prob: FCN에 의해서 feature map인 $p$가 나온다. 해당 $p$는 각각 너비, 높이 그리고 채널에 해당하는 $w,h,d$를 가진다.
Gallery: spatial feature map인 $g_c$는 FCN에 의해서 gallery의 $c$에서 feature 가 추출되어 나온다.

명백하게, prob와 Gallery의 차원이 불일치하면 계산을 할 수가 없다. 따라서, Gallery의 feature map인 $g_c$에서 prob의 feature map인 $p$ 만큼 sliding window로 잘라낸다. 위의 그림 2에서 보이는 것처럼 k개의 sub-feature maps은 $G_c = [g_{c_1},g_{c_2},...,g_{c_k}]$로 나타낼 수 있다. $G_c$는 probe 크기에 따라 $G_c \in \mathbb{R}^{M\times k}$이다.
정렬없이 feature matching을 위해서 $p$가 $G_c$의 선형 결합으로 표현되는 error reconstruction으로 문제를 바꿀 수 있다. 따라서, $G_c$에 관한 p의 계수를 계산할 것이다. 그리고 그 계수를 $w_c$로 표현한다. reconstruction error를 matching score로 표현할 수 있으며 최종적으로 $w_c$를 풀기위해서는 reconstruction error를 최소화 해야한다.
$$
\mathcal{L}(w_c)=||p-G_cw_c||_2^2
$$
$w_c\in \mathbb{R}^{k+1}$과 $p \in \mathbb{R}^{M+1}$이다. $w_c$를 구하기 위해 2가지 제한조건이 있는데 sparsity와 similarity 이다.

Sparse constraint는 feature vector $p$로 부터 나온 coding vector $w_c$의 sparsity를 컨트롤한다. 따라서, $w_c$는 $l_1-norm:\ ||w_c|| _1$을 사용한다.

Similarity-guided constraint.
feature $p$를 재구성한 sub-feature를 자유롭게 사용하는 재구성 프로세스에는 단점이 있다. $G_c$의 선형 조합을 위해 재구성 에러를 최소화하기 위해서 재구성 프로세스에만 집중하기 때문에 $p$와 feature vector $G_c$의 유사도를 고려하지 않는다. 즉, 재구성 에러를 최소화에 집중하기 때문에 비슷하지않은 feture vector들이 선택될 수 있다.
$p$와 $G_c$의 유사도를 계산하기위해 $l_2-norm$으로 1에 가깝게 정규화를 한다. 그러면 유사도 점수 벡터인 $p^TG_c \in \mathbb{R}^{1\times k}$는 cosine similarity measure이 된다. 이렇게 되면 유사ㅣ하면 더 많은 $g_c$가 선택되고 아니라면 제외된다. 즉, $p^TG_c$는 연관성을 보여준다. 그 후, similarity-guided constraint인 $p^TG_c W_c$가 정의된다.

최종 sparse representation formulation은 다음과 같다.
$$
L(w_c)=||p-G_cw_c||_2^2-\alpha^TG_cw_c+\beta||w_c||_1
$$
$\alpha$ 와 $\beta$는 각각 similarity-guided constraint 와 sparsity constraint을 나타낸다.
그 후에, $w_c$를 최적화 하기위해서 다음과 같이 변형한다.
$$
L(w_c)=\frac{1}{2}w_c^TG_c^Tw_c-(1+\frac{\alpha}{2})p^TG_cW_c+\frac{\beta}{2}||w_c||_1.
$$
$w_c$를 구하기 위해서 feature-sign search algorithm [14][14]를 사용하는데, $w_c$에서 Non-zero 값은 선택된 sub-feature vectors이다.
그리고 dynamic matching method를 적용해 probe와의 유사도를 검증한다.
$$
\underset{c}{min}\ r_c(p)=||p-G_cw_c||_2-\alpha^TG_cw_c.
$$
위의 수식은 reconstruction error와 weighted matching scores을 퓨전 합 한 것이다.

새로운 probe를 증명해야할 때, gallery feature map들을 다른 크기의 probe 이미지에 따라서 재분해한다. 따라서, gallery를 동적으로 사용할 수 있다. 또한, FCN의 몇며 layer들은 매우 효과적으로 output feature map 크기를 줄이기 때문에 효율성도 좋다.
논문에서는 probe의 크기가 $5\times5$이라면, $g_c$의 크기는 $7\times 7$이 되고, stride는 1 그리고 decomposition operation 인 $k=9$로 설정하면 된다고 한다.
DFM은 빠르게 feature를 뽑아낼 수 있으며, alignment-free method이며 다양한 크기의 probe로 부터 face recognition이 가능하다고 한다.

3.3 Sliding Loss

식 2에서는 FCN의 파라미터들은 고정되어있다. 따라서, 계수 $w_c$와 convolution parameters 인 $\theta$를 학습하기위해 Sliding Loss를 사용한다. 해당 Loss는 식 2를 최소화함으로써 나오는 deep feature들의 구분성을 계선하는데 사용한다.
$$
L(w_c,\theta)=y_c(||p-G_cw_c||^2_2-\alpha p^TG_cw_c)+\beta||w_c||_1.
$$
여기서 $y_c$가 1이면 $p$와 $G_c$는 같은 identity를 가지고 있는 것이며, $||p-GW||_2^2-\alpha p^TG_cw_c$를 최소화 하는 것이다. $y_c$가 -1이면 $p$와 $G_c$는 다른 identity를 가지고 있는 것이며, $-||p-GW||_2^2-\alpha p^TG_cw_c$를 최소화 하는 것이다.

3.4 Optimization.

처음에 $w_c$을 최적화하고 그 뒤에 $\theta$를 최적화 한다.
Step 1: fix $\theta$, optimize $w_c$.
reconstruction coefficients인 $w_c$를 feature-sign search algorithm을 사용해 학습시키는 것이다.
식 5를 변경한 것이다.
$$
L(w_c)=\frac{1}{2}y_cw_c^TG_c^TG_cw_c-y_c(1+\frac{\alpha}{2})p^TG_cw_c+\frac{\beta}{2}||w_c||_1,
$$

Step 2: fix $w_c$, optimize $\theta$.
FCN을 update 하면서 discrimintative feature들을 얻을 수 있다. $||p-G_cw_c||^2_2$는 $p$가 선택된 모든 sub-feature map 과의 근접함을 알 수 있다. $\alpha^TG_cw_c$는 p와 각 sub-feature map과의 거리를 줄여주는 것을 목표로 한다.
위의 2개 개념은 deep feature들의 구별성을 증가시켜 준다. 따라서, $p$와 $G_c$로 $L(\theta)$를 미분 하면
$$
\begin{cases}
& \frac{\partial L(\theta)}{\partial p}=2(p-G_cw_c)-\alpha G_cw_c \newline
& \frac{\partial L(\theta)}{\partial G_c}=-2(p-G_cw_c)w_c^T - \alpha w_c^T.
\end{cases}\
$$
$p$와 $G_c$는 같은 FCN 파라미터 $\theta$를 공유한다. 그림 3과 같이 연쇄적으로 구해진다. 그 후에 SGD로 FCN이 학습이 된다. 학습 알고리즘은 Alogorithm 1에서 볼 수 있다

본 논문에서는 통합된 프레임워크를 설명했으며, softmax loss와 비교해서 전체 얼굴에서 임의의 얼굴 이미지 사이 거리 정보를 더 잘 표현할 수 있다고 한다.

4.Experiments

Network Architecture.: VGGFace에서 non-convolutional layers들을 다 제거하고 13층의 convolutional layers을 사용하였다. 마지막 pooling layer은 feature extractor이다. 표 1에서 전체 구조를 확인 할 수 있다.

Training and testing. : 그림 4를 보면 전체적인 구조를 볼 수있다.

• 16GB RAM, i7-4770 CPU @ 3.40GHz 장비를 사용함.
• CASIA-WebFace dataset에서 FCN과 sliding loss를 사용함.
• 각 랜덤 사이즈의 얼굴 이미지와 5개의 전체 얼굴 사진이 1그룹으로 2000개의 그룹이 존재한다.
• batch는 20 $10^{-4}$의 learning rate, $\alpha=0.6, \beta=0.4$

test를 진행 할 대는, probe와 gallery를 1가지 셋으로 사용하였다. FCN으로 특징을 추출하고 식 3과 식 7을 통해 얼굴인식을 진행하였다.

Evaluation Protocol: 제한한 방법의 성능 평과를 위해 Cumulative Match Characteristic (CMC) curve 실험과 Receiver Operationg Characterisitc (ROC) curve 실험을 진행하였다.

Databases and Settings.

• 학습에 partial-LFW를 사용하였다. LFW는 7,749명의 13,233 이미지가 포함되어 있는데, 많은 장애요소 (조명, 방해물, 각도 등)이 있따. 따라서, gallery face image는 $224\times224$로 재조정하고 probe는 전체 얼굴 이미지에서 랜덤으로 잘라서 사용한다.
  

  

• evaluation에는 partial-YTF를 사용하였다. YTF는 1595명의 3,424개의 비디오들이 포함되어있다. gallery는 200명에 대한 200개의 얼굴 이미지로 사용했으며, probe는 임의의 크기로 전체 얼굴에서 잘라서 사용한다.
• CASIA-NIR-Distance dataset 또한 evaluation에 사용한다. partial face image인 동시에 여러 각도와 크기 그리고 빛 상태를 가진다. 그림 5에서 확인 할 수 있다.

4.2 Experiment on LFW

4.2.1 Comparison to the State-of-the-Art

SOTA 비교를 위해 4개의 SOTA와 비교를 했다.

• Multi-Scale Region-based CNN (MR-CNN) 10, MKDSRC-GTP 43, I2C 11 그리고 probe를 $224 \times 224$로 re-scaling한 VGGFace 이다. 본 논문에서 DFM은 $\alpha=2.1$ and $\beta=0.1$ 이다.
  표 2를 보면 DFM의 성능을 볼 수 있다. keypoint 기반의 알고리즘은, no robust하기 때문에 적절하지 않고, MR-CNN의 경우 alignment가 필요하며 CNN을 사용하지만 들인 시간만큼 성능이 나오지 않는다. 특히, 전통적인 방법으로는 임의의 크기를 가지는 얼굴 이미지들을 고정된 이미지로 조정해야한다.
  $224 \times 224$ VGGFace는 DFM보다 성능이 낮은데, 크기를 바꾸면서, 불필요한 기하학적 변형이 일어나기 때문이다. DFM은 변형없이 공간 정보를 유지한다.

  4.2.2 Face verification on LFW
• Face verification은 얼굴 이미지 짝으로 부터 같은 사람인지 아닌지 확인하는 기술이다. 본 논문에서는 LFW의 test protocol을 사용했다. 데이터셋을 cross-validation으로 10개의 subset으로나누고 각 subset은 300개의 진짜/가짜를 이룬다. 부분 얼굴 이미지를 위해 임의의 크기로 랜덤하게 자른다.

그림6은 다양한 PFR 알고리즘에 대한 ROC curve를 나타낸다. DFM은 다른 알고리즘에 비해 제일 좋은 성능을 보이며, 0.19ㅊ초라는 획기적인 속도를 보여준다.

4.2.3 Evaluation on holistic face images and mixed partial and holistic face images

LFW에 대해 추가적인 실험을 진행햇는데, 총 3가지 그룹으로 나눠서 했다.

1. Probe-1: 1000개의 전체 얼굴 이미지
2. Probe-2: 500개의 전체 얼굴 이미지와 500개의 부분 얼굴 이미지
3. Probe-3: 1000개의 부분 얼굴 이미지

표 3에서 결과를 보여주고 있다.

4.2.4 Influence of the cropped region size and the area

그림 7은 다른 크기의 얼굴 이미지에 따른 결과를 나타낸다.

그림 8은 어굴이미지의 다른 영역의 예제를 보여준다.

표 4는 그림 8의 예제를 가지고 실험한 결과를 보여준다.

위의 결과가 나오는 것은 당연하다. 잘라진 이미지는 더 적은 공간 정보를 갖고 있기 때문이다. 하지만, 눈 위로의 정보를 가질 경우, identification에 있어 좋은 성능을 보인다.

4.2.5 Parameter Analysis

similarity-guided constraint 인 $\alpha$와 sparsity constraint 인 $\beta$에 대한 실험도 진행했다. $\alpha$의 경우 0에서 4.2까지 0.3만큼 조절 했으며, $\beta$의 경우 0.1에서 1까지 0.1씩 조절했다. 그림 9는 DFM에 대한 $\alpha$와 $\beta$의 영향을 보여주면 best 는 $\alpha=2.1$과 $\beta=0.1$이다.

4.3 Partial Face Recognition on CASIA-NIR-Distance and Partial-YTF

CASIA-NIR-Distance와 Partial-YTF에 대한 성능 비교를 실험하였다. DFM, MKDSRC-GTP, RPSM, I2C, VGGFace 그리고 FaceNet에 대한 비교이다. 밑의 표 5를 보면 확인할 수 있다.

1) key-point 기반의 알고리즘은 부분 얼굴 인식에서 robust하지 못하기 떄문에 성능일 떨어지는 것으로 보인다.
2) VGGFace의 경우 고정 이미지로 변환하는 과정에 변형이 일어나 성능이 내려가는 것으로 보인다.

5. Conclusion

FCN은 모호한 입력사이즈로 부터 계산량 공유를 통해 부분적인 featur들을 생산한다. 또한 SRC를 사용해 alignment-free matching을 가능하게 했으며 FCN이 만든 feature를 잘 구별하는 DFM에 근거한 sliding loss를 제안했다.

EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks

Mingxing Tan Quoc V.Le

Abstract

ConvNet들은 공통적으로 고정된 자원안에서 계발되고 그 후에 더 좋은 정확도를 위해 이용가능한 자원을 사용한다. 본 논문에서는 네트워크의 깊이, 너비, 그리고 해상도를 적당히 조절하여 더 좋은 성능을 가져옴을 연구했다. 해당 요소를 'compound coefficient'라고 한다.
또한, neural architecture search 기술을 이용해 EfficientNet이라는 베이스라인을 사용했으며, 8.4배 더 작고 6.1배 더 빠른 내트워크를 만들었다. 물론, SOTA도 기록했다.

1. Introduction

Scaling을 통해 정확도를 올리는 것은 옛날부터 이어져왔다. ResNet이나 GPIpe 같은 모델들이 있다. 현재 scaling 방법에는 총 3가지 정도가 유행하는데, depth (ResNet [1][1]) , width (Wide ResNet [2][2]) 그리고 resolution (Gpipe [3][3]) 이 있다. 위의 3가지 차원을 임의로 scaling 하는 것은 지루한 tuning이 되고 그것 또한 sub-optimal accuracy와 efficiency 일 것이다.

논문에서는, ConvNet scaling 과정에 대해서 다시 생각해보고 연구했다. 주요 물음은 "더 좋은 정확도와 효율성을 달성하기 위해 ConvNet을 scaling하는 원칙에 입각한 방법이 있을까?" 이다. 고정된 비율로 각 요소에 대해 scaling을 하면 적절한 balance를 가질 수 있다. 이러한 방법을 Compound Scaling Method라고 한다. 이 방법은 공평하게 네트워크의 너비, 깊이 그리고 해상도를 scaling 하는 것이다. 예를 들어 제한된 자원이 $2^N$이라면, 깊이는 $\alpha^N$, 너비는 $\beta^N$ 그리고 해상도는 $\gamma^N$이다. 상수의 계수는 original model에서 grid search를 통해서 결정된다. 밑의 그림에서 확인 할 수 있다.

직갑적으로, 복합체 scaling 방법은 의미가 있다. 본 논문은 width, depth 그리고 resolution 세가지 사이의 관계에 대해 수량화한 첫번째 논문이다.

특히, 모델 scaling의 유효성은 베이스라인 네트워크에 의존 적인데, NAS를 사용해 EfficientNet을 베이스라인으로 사용했다. 그림 1을 보면 현저한 차이를 볼 수 있다. 이 때 당시의 최고 성능인 GPipe [3][3] 보다 8.4배 작은 파라미터를 가지며, 6.1배 더 빠르다. 또한,** EfficientNet들은 ImageNet에서 학습한 후 transfer learning을 통해 다른 데이터 셋에서도 좋은 성능을 보임을 보였다.**

2. Related Work

ConvNet Accuracy: AlexNet을 시작으로 ConvNet들은 정확도를 올리기 위해 더욱 더 커져갔다. 최근에는 GPipe 라는 제일 좋은 성능을 가지는 네트워크가 나왔는데, 특별한 pipeline parallelism library를 사용해 네트워크를 나누고 다른 accelerator를 각 부분에 분배하는 방식을 사용한다. 또한, ImageNet에서 성능이 좋으면 다른 데이터 셋으로 transfer learning에서 좋은 성능을 보였다. 하지만, 더 높은 정확도가 중요하지만, 하드웨어 메모리에 제한은 있으므로, 더 좋은 효율성을 얻는 것이 중요해졌다.

ConvNet Efficiency: Deep ConvNet들은 너무 과도한 파라미터들을 가진다. 따라서 모델 압축 기술이 나왔는데 [4][4], [5][5], 그리고 [6][6] 등이 있다. 또한, 직접 모델을 구축한 ,SqueezeNet, MobileNet 그리고 ShuffleNet 등이 있다. 최근에는 NAS가 등장해 효과적인 모바일 크기의 ConvNet ( [7][7] [8][8] )등이 등장 했으며 사람이 디자인한 ConvNet들 보다 더 좋은 성능을 보인다. 본 논문에서는 SOTA에 대한 모델 효율성에 집중한다. 그 후에 scaling에 따라 재분류한다.

Model Scaling: ResNet ([1][1]) 과 같은 모델은 네트워크의 깊이에 대해 신경을 썼으며, Wide ResNet ([2][2])과 MobileNet ([9][9])은 네트워크의 너비에 대해 신경을 썼다. 또한, 입력 해상도가 클 수록 좋은 성능을 보이는 것은 잘 알려진 사실이다. 과ㅏ거의 논문들은 깊이와 너비가 다 중요하다고 하지만 여전히 효율성과 정확도를 더 좋게하는 것에 대한 연구는 지속적으로 진행중이다. 본 논문에서는 ConvNet에 대한 너비, 깊이 그리고 해상도의 모든 차원 scaling에 대한 연구이다.

3. Compound Model Scaling

본 섹션에서는 scaling 문제를 공식화 하고 다른 접근법에 대해 소개하고 논문에서 만든 새로운 scaling method를 소개한다.

3.1 Problem Formulation

ConvNet Layer를 $i$라고 할 때, $Y_i=F_i(X_i)$ 이라고 할 수 있다.
$F_i$는 operator, $Y_i$는 출력, $X_i$는 입력 그리고 tensor 모양은 $<H_i, W_i, C_i>$ 이다. 따라서, ConvNet을 다음과 같이 나타낼 수 있다: $N=F_k \odot...\odot F_2 \odot F_1(X_1)=F_k \odot_{j=1...k}F_j(X_1)$
보통 Deep convNet의 경우 각 stage와 같은 구조를 가진다. ResNet의 경우 5개의 stage로 나눠져잇으며, 다운 샘플링을 하는 부분을 제외하고 같은 convolutional type을 가진다. 따라서 밑의 수식과 같이 ConvNet을 표현할 수 있다.
$$
N=\odot_{i=1...s}F_i^{L_i}(X_{<H_i,W_i,C_i>})
$$
i stage에서 $F_i$ layer가 $L_i$번 반복 되는 것을 뜻한다. fig2 (a)는 전형적인 ConvNet을 보여주며, 점점 spatial dimension이 작아지지만, Channel의 수는 증가한다.

일반적인 ConvNet을 디자인 하는 것과 다르게, 본 논문은 네트워크 layer의 구조가 아닌, lenghth, width 그리고 resolution을 변경한다. 물론, 고정적인 상수를 두고 비율을 변화시키는 방법을 사용하였다. 이것을 공식화하면:
$$
\max_{d,w,r} Accuracy(N(d,w,r)) \\
s.t. \quad N(d,w,r)=\odot_{i=1..s} \hat{F}i^{d \cdot \hat{L_i}} (X{<r\cdot \hat{H}_i, r\cdot \hat{W}_i,r\cdot \hat{C}_i}) \\

Memory(N)\leq target_memory \\
FLOPS(N)\leq target_flops
$$

w,d,r 은 각각 width, depth 그리고 resolution을 뜻하며 $\hat{A}$이 들어간 것은 이미 정의된 베이스라인 네트워크를 뜻한다.

3.2 Scaling dimensions

d, w, r은 서로서로 의존적이고 다른 resource constraints 아래에서 바꿔야함으로 scaling이 매우 어렵다. 각각은 다음과 같이 scaling 한다.
Depth (d): scaling network depth는 ConvNet의 정확도를 올리는 간편한 방법중 한가지이다. 하지만, 깊은 네트워크 일수록 gradient vanishing 문제를 해결하기가 어렵다. 하지만, Skip connection과 batch normalization이라는 방법이 나왓지만, 그래도 여전히 깊어질 수록 무조건 좋은 성능을 가져오는 것은 아니다.

Width (w): 더 넓은 너비를 가지는 네트워크는 쉽게 학습되고 fine-grained feature들을 잘 추출할 수 있다. 하지만, higher level feature들을 봅아 오는 걸 어려워하는 경향이 있다.

Resoultio (r): 더 큰 해상도는 더 많은 fine-grained pattern을 찾을 수 있다. 299x299 (Inception), 331x331 그리고 480x480 (GPipe)에 이르는 해상도를 가진 네트워크들도 있다. 하지만, 매우 높은 (560x560) 해상도에서는 도리어 정확도가 떨어지는 경향이 있다.

Observation 1: 너비, 깊이 그리고 해상도를 증가시키면 정확도가 상승하지만 도리어 매우 클 경우 정확도 상승이 없어진다. -> 즉, 적당한 크기가 존재한다는 것이다.

3.3 Compound Scaling

실험적으로, 다른 scaling dimensions들이 의존적이라는 것을 관찰했다. 직관적으로, 더 큰 해상도에서 더 깊은 네트워크나 넓은 네트워크의 정확도가 좋을 것이다. 따라서, 본 논문에서는 단일 dimension에 대해 실험을 진행한 것이 아니라, 여러 조합을 사용해 진행하였다.

위의 그래프를 살펴보면 깊이만 늘린 것보다 해상도와 함께 깊이를 올리는 것이 더 좋은 성능을 가져온다.

Observation 2: 더 좋은 정확도와 효율성을 추구하기 위해서는 너비, 깊이 그리고 해상도를 적절하게 scaling 해야한다.

본 논문에서는 새로운 compound scaling method를 제안하며 compound coefficient $\phi$로 표현한다.
$$
depth:\ d=\alpha^{\phi} \
width:\ w=\beta^{\phi} \
resolution:\ r=\gamma^{\phi} \
s.t \quad \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \
\alpha \geq1,\beta \geq1, \gamma \geq1
$$

$\alpha,\beta,\gamma$는 grid search를 통해서 결정된다. 일반적으로 FLOPS는 $d,\ w^2,\ r^2$의 배율로 증가한다. 본 논문에서 새로운 $\phi$로 제한을 햇으며, 전체적인 FLOPS는 대략적으로 $2^\phi$만큼 증가한다.

4. EfficientNet Architecture

model scaling은 베이스라인 네트워크를 바꾸는 것이 아니기 때문에, 새로운 mobile-size baseline 인 EfficientNet을 만들었다.

MNAS ([7][7])에서 영감을 얻어 같은 search space와 $ACC(m) \times [FLOPS(m)/T]^w$를 사용했다. $T$는 목표하는 FLOPS 이며 $w=-0.07$로 정확도와 FLOPS 사이를 제어하는 하이퍼 파라미터이다. MNAS랑은 다르게 지연속도보다는 FLOPS를 최적화 하는데 목표를 두었다. 따라서 EfficienNet-B0가 나왔으며, MNASNet과는 유사하지만, 조금 더 많은 FLOPS를 가진다. 밑의 표1에서 구조를 확인할 수 있다. mobile inveted bottleneck인 MBConv를 주요 block으로 두고 squeeze-and-excitation ([10][10]) 최적화도 추가했다.

밑의 2가지 단계를 거쳐 scaling 된다.

• STEP 1: $\phi=1$로 고정하고 grid search를 통해 $\alpha,\beta,\gamma$를 수식 2, 3에서 찾는다.
• STEP 2: $\alpha, \beta, \gamma$를 고정한뒤 다른 $\phi$를 적용하여 수식 3을 완성한다.

간략하게 요약하면, 작은 베이스라인 네트워크를 찾고 (STEP 1) 적절한 scaling coefficient들을 찾는다. (STEP 2)

5. Experiments

5.1 Scaling Up MobileNets and ResNets

당시에 대표적인 ConvNet들인 mobileNet과 ResNet에 대한 scaling method를 적용하고 비교했다. 밑의 표3에서 확인할 수 있다.

5.2 ImageNet Results for EfficientNet

첫 문단에서는 ImageNet을 학습하는 환경에 대한 설명들이다.

• RMSProp optimizer, decay: 0.9, momentum: 0.9
• BN 사용, momentum: 0.99
• weight decay: 1e-5
• Initial learning rate: 0.256, 매 2.4 epoch 마다 decay:0.97
• SiLU (Swish-1) 사용
• AutoAugment 사용
• 잔존확률: 0.8로 stochastic depth 사용
• dropout 사용, 0.2(B0) ~ 0.5(B7)
• trainingset에서 25K를 minival set으로 사용
• validation 도중 최종 validation accuracy 도달 시 early-stopping

위의 표를 보면 비슷한 정확도에서 좀 더 효율적인 구조를 가지는 것으로 확인할 수 있다.

그림1과 그림 5를 비교하면 EfficientNet이 더 작고 효율적이라는 것을 확인할 수 있다.

지연시간 평가를 했으며, 위의 표 4를 보면 확인 할 수 있다.

5.3 Transfer Learning Results for EfficientNet

위의 표6을 보면 transfer learning에 사용한 데이터셋에 대해서 볼 수 있다.

위의 표5를 보면 tranfer learning에 대한 결과를 볼 수 있다.

1) 유명한 모델들인 NASNet-A 와 Inception-v4 에 대한 결과를 비교 했다.
2) 당시 SOTA 인 Gpipe에 DAT를 적용한 것과 비교를 했다.

마지막으로 밑의 그림 6을 보면 각 데이터 셋에서 EfficientNet이 얼마나 효율적인지를 볼 수 있다.

6. Discussion

Efficient 모델과 scaling method에 대한 공헌을 구분하기위해 그림 8을 보면 확연하게 알 수 있다. 다른 scaling method와의 비교를 통해 본 논문에서 제안한 scaling method가 더 효율적인 것을 알 수 있다.

또한 그래프상이 아닌 activation map을 통한 비교를 그림 7에서 볼 수 있다. 확연하게 compound scaling method가 더 잘 나타내는 것을 알 수 있다.

7. Conclusion

깊이, 너비 그리고 해상도를 밸런스있게 하는 것도 중요하지만, 더 나은 정확성과 효율성을 방해한다는 사실을 발견했다. 본 논문에서는 더 적은 FLOPS와 더 좋은 성능을 가진 EfficientNet 모델을 발견했다.

[1]: https://arxiv.org/abs/1512.03385 ""ResNet""
[2]: https://arxiv.org/abs/1605.07146 "Wide ResNet"
[3]: https://arxiv.org/abs/1811.06965 ""GPipe""
[4]: https://arxiv.org/pdf/1510.00149.pdf "Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding"
[5]:https://arxiv.org/abs/1802.03494 "Amc: Automl for model compression and acceleration on mobile devices"
[6]:https://arxiv.org/abs/1804.03230 "Netadapt: Platform-aware neural network adaptation for mobile applications"
[7]:https://arxiv.org/abs/1807.11626 "MNASNet"
[8]:https://arxiv.org/abs/1812.00332 "ProxylessNAS: Direct Neural Architecture Search on Target Task and Hardware"
[9]: https://arxiv.org/abs/1704.04861 ""MobileNet""
[10]: https://arxiv.org/abs/1709.01507 ""SENet""

Attack to Explain Deep Representation

[

Attack to Explain Deep Representation - IEEE Conference Publication

ieeexplore.ieee.org

](https://ieeexplore.ieee.org/document/9156888)

Mohammad A. A. K. Jalwana Naveed Akhtar M. Bennamoun A. Mian

University of Western Australia

Abstract

Deep visual model들은 입력 이미지의 극히 작은 변화에도 민감하다. 따라서, 본 논문에서는 모델을 공격해 바보처럼 만드는 것이 아닌 학습된 representation을 설명하는 것에 집중하는 첫 논문이다. 처음의 작은 변화가 나중에는 눈에 띄일 정도로 커지는 것을 확인할 수 있다. 본 저자들은 이러한 변화를 robust classifier에 공격을 함으로써 이미지 생성, 인페이팅 그리고 interactive image manipulation에 적용했다.

1. Introduction

deep model들은 적대적인 작은 변화에 대해서 취약하다. 특히, 사람이 인지못하는 추가적인 작은 신호를 통한 변화에도 약하다.
두 가지의 접근법이 있다.

1) 작은 변화를 생성하거나 높은 전도성을 통해 deep models을 멍청하게 만드는 것
2) 작은 변화에 반대해서 model을 방어하는 것

또한, 합성을 통해 적대적으로 robust한 network를 만드는 논문도 있다. -> 이건 꼭 보기[41]

[19]에서는 ImageNet과 같이 큰 데이터셋에서 사람이 인지하지못하고 불안정하지만 예측할 수 있는 feature들이 있다고 인정했다. 이렇게 non-robust feature에 의존적인 deep model들은 당연히 작은 변화에 민감할 수 밖에 없다. 이런 것을 미루어보아 사람의 인지와 deep visual representation 사이에는 큰 차이가 있는 것 같다. 따라서, [14]에서는 robust optimizer framework를 제안했지만, 기존의 것보다 계산량이 급격한 증가를 보인다.

인간의 지각과 일치하지않은 representation이 여전히 인간 의미 visual task에서 높은 정확도를 가지는 것이 역설적이다. 그림 1 (top) 을 보면 적대적인 작은 변화가 포함된 상태로 분류를 하면 완전히 다른 라벨로 분류되며 salient visual feature에서도 확인할 수 있다. 하지만, salient visual feature들을 보면 사람이 사물을 인지하는 것과 deep model들이 인지하는 것에 큰 차이가 없어보인다. 오히려 원시적이고 감지하기 힘든 형태이기는 하지만, 적대적인 작은 변화를 대상 라벨의 인간 의미 가하학적 feature들로 볼 수 있다. -> 다시 해석하자면, 적대적인 작은 변화는 인간이 알아차리기 힘든 형태지만 라벨에 해당하는 feature을 가지게되는 것이라고 볼 수 있다. 이것으로 미루어보아 deep model들도 인간이 사물에서 특징들을 인식하는 것처럼 작동하는 것으로 볼 수 있다.

본 논문의 변화 평가 알고리즘은 확률적으로 주어진 대상 라벨에 이미지 분산에 의해 변화된 샘플의 예측 확률을 극대화한다. 본 저자들은 변화 신호를 분류기의 깊은 층에 있는 매우 활동적인 뉴런들에 집중하기 위해서 연결한다. 그림 1에서 확인할 수 있다.

게다가, deep model들이 이미지에서 집중적으로 보는 visual feature들을 설명하고 인간의 지각과 deep representation의 일치를 위해서 자연스럽게 low-level task에 집중하게되었다. e.g 이미지 생성, 인페이팅 그리고 interactive image manipulation.

본 논문의 major contribution:

1) attack technique을 fooling이 아닌 설명을 위해 사용함
2) non-robust model들에 작은 변화를 줘서 나온 salient visual feature들로 미루어보아, 인간의 인지와 deep models의 인지에는 차이가 없을 것 같음을 보여줌
3) 이미지 생성, 인페이팅 그리고 interactive image manipulation에 실험을 진행함. 왜냐하면 자연스럽게 low-level을 탐구하게되어서

2. Related Work

[2] adversarial attack에 관한 논문.

Adversarial attcks: 초창기에는 Szegedy [45]에서 시작했으며, Goodfellow가 FSGM[16]을 시작으로 I-FGSM[25], MI-FGSM[[13][13]], D$I^2$-FGSM[[51][51]] 그리고 vr-IGSM[48]이 나왔다.

위의 논문들과 다른 여러 논문들은 사람한테는 noisy로 보이지만 완전하게 모델을 멍청하게 만드는 것에 집중했으며 많은 이미지를 오분류하게 만드는 noisy인 Universal Advesarial perturbation인 [29]도 나왔다. 따라서, 실질적으로 high-level에 사용하는 분류기에도 이러한 위협이 가깝게 다가오기 때문에 현재 활발하게 연구 되고있다.

Adversarial defenses: adversarial attack에 대항하여 model에 들어오는 변화를 감지하고 막는 기술이다. 하지만, 강력한 adversarial attack이면 이러한 defenses도 뚫을 수 있다.

Non-adversarial perspective: adversarial attack을 공격용도가 아닌 해석용도로 사용한 논문 들도 있다. [46][46]과 [47][47]이 대표적인데, adversarially robust models들을 바보로 만드는 작은변화 신호를 salient visual feature의 존재를 관측했다. 이러한 것을 통해 model을 설명하는 것이다. 그러나, 몇몇 논문에서는 deep representation과 인간 지각이 일치 하지 않음을 주장한다. [14][[46][46]]
???? 번역기 돌린거... 이해가 안됨: 잠재적으로 재정렬은 오직 심각한 성능 손실과 컴퓨팅 복장성의 증폭으로 모델을 적대적으로 강건하게해야만 달성 할 수 있다.[14] [[46][46]].

3. Attacking to explain

Adversarial attack에서는 Deep visual classification model을 통과할 때, 잘못된 label로 구별하는 것을 목표로 한다. 식으로 나타내면,
$$
\kappa(\iota+p) \rightarrow \mathcal{l}_ {target} \ s.t. \ \mathcal{l}_ {target} \neq \mathcal{l}_ {true},||p||_p \leq \eta,
$$
$\kappa$는 Deep visual classification model, $p$는 perturbation, $||p||_p$는 norm을 뜻하며, $\eta$에 의해 제한된다.

위의 (1)를 보면, $\kappa$와 $I$로 $p$를 표현할 수 있으며, $\kappa$가 고정된다면, 이미지의 특정한 변화를 계산하기 위해 $p$의 도메인을 국한한다. 하지만,이런 제한은 단 하나의 데이터에 대한 특질만 반영하여 전체적인 분류기의 성질을 나타내기 어렵다. 또한, 이미지의 특정한 변화를 통한 인간의 지각과 deep representation 사이의 어긋남에 대한 의문을 제기할 수 있다. 작은변화와 함께 분류기의 특성을 더 잘 보여주기 위해서는 신호에 대해 변하지않는 입력 샘플이 필요하며, p의 영역을 확장하여 달성할 수 있다.

universal perturbations [29]와 같은 논문은 본 논문과 비슷한 내용을 담고 있는데, 많은 이미지에 대해서 처리할 수 있지만, salient feature map을 보면 기하학적인 모양은 매우 틀리다. 아마도, 특정한 물체가 아닌 무작위 class로 할당되도록 만들어서 그렇다. 주어진 Deep model ($\kappa$)에 'targeted' 목적으로 pertubation 영역을 넓히는 것은 Deep model $\kappa$에 의해 실제로 target의 특징이 두드러지게 p의 기하학적 패턴을 유도할 가능성이 있다.
--> 즉... p가 target의 기하하적 특징을 가지도록 유도할 수 있다.

(1)의 식에서 $l_{target}$을 매핑하는 $\kappa$의 확률을 최대하 하는 것으로 바꿀 수 있다. 즉, 모든 샘플들을 포함해서 최대화해야한다.

$$
\mathbb{E}[P(\kappa(I + p) \rightarrow l_{target})] \geq \gamma, \ s.t \quad
Dom(p) = {\forall I|I \backsim \mathcal{I}}, |Dom(p)| \gg 1, ||p||_p \leq \eta,
$$
$\gamma \in [0,1]$을 만족하며, (2)를 만족하는 $p$에는 위의 예시에 대한 명백한 정보가 드러내질 것으로 예상된다. (Dom은 정의역을 나타낸다.)

다음과 같은 질문이 생길 것이다.

1) 모델로 물체의 구별할 수 있는 시각 특징으로 여겨지는 게 무엇인가?
2) 모델의 주어진 label index는 의미론적으로 어떻게 볼 수 있는가?
3) feature들과 semanitcs가 인간 해석적이라고 볼 수 있을까?

4. Algorithm

2가지 단계로 나눠진다.

1) perturbation estimation: 전체론적으로 작은 변화가 목표 클래스의 구별가능한 feature들로 유도되도록 하는 것.
2) perturbation refinement: 이미지 구역들에서 작은변화가 더 많은 뉴런 활동을 할 수 있도록 하는 것

Perturbation estimation: perturbation 영역의 확장을 위해 입력의 분산이 필요하다. 입력 $I$는 다음과 같은 공식으로 결정된다. $\mathfrak{F} = {d} \cup \bar{D}$. $d$는 seed 이미지인 반면에 D는 입력으로 부터 온다. Perturbation estimation은 Algorithm.1 에서 확인할 수 있다. SGD를 사용한다.
$$
max_p \mathfrak{H}=\mathbb{E}_ {I \sim \mathfrak{F}} [P(\kappa(I + p)) \rightarrow l_{target}] \quad s.t. \ ||p||_2\leq \eta.
$$

핵심적으로, 알고리즘은 위의 공식인 (3)을 해결하기위해 시각적 모델의 cost surface 의 다단계 순회를 위한 분산 샘플의 mini-batch를 사용한다. 밑의 algortihm 1은 gradient monet와 mini-batch의 surface를 미분을 해 $\mathfrak{F}$을 최대화한다. 즉, SGD와 Momentum을 통해서 위의 (3)식을 최대화 한다. $\mathfrak{F} \geq \gamma$가 되도록 한다.

알고리즘을 설명하면
line 2: mini-batch인 b에서 -1을 한 b-1만큼 데이터 샘플을 뽑고
line 3-4: seed d와 최근의 perturbation을 샘플에 둘러싼다. 이 cliping은 0에서 1사이로 샘플을 국한시킨다. $\ominus$는 샘플이나 set에서 각각의 요소에 perturbation을 적용시키는 것을 뜻한다. 반복문 안에서는 SGD로 작동한다.
seed는 입력을 변경하여 perturbation의 변화를 허용하기 위해 알고리즘에 사용된다. 입력 샘플에 대한 제한을 정하지 않으며, D와 d가 매우 다를 수 있음을 나타낸다. 또한, $l_{traget}$에 직접적으로 gradient를 구한 것이 $d$에 계산된 것과 현저하게 다를 수 있음을 나타낸다. (denoted $\triangledown_{d_i} \mathcal{J}(d_i, l_{targe}))$
line 6: 이 차이를 설명하기위해, $d_i$에 대한 gradient norm을 $d_i \in D$의 평균으로 나눈 비율을 구한다.
line 7: 6에서 구한 비율을 여기서 결합하는데, seed gradient과의 높은 관련성을 얻기위해서 사용된다.
line 8-9: 위의 합성된 gradient로 first and second raw moment를 추산하는데 $\alpha$와 $\beta$로 조절한다. 위의 moment는 Adam algorithm으로 부터 영감을 받았다. 경험적으로 hyperparameter들의 영향이 비슷하며 Adam의 값으로 고정한다. -> 이것은 line 1에서 확인할 수 있다. 다른 값들은 0으로 초기화하는데 $\alpha$ 와 $\beta$만 특정한 값을 가진다.
line 10: 이동평균법을 적용 시킨 것
line 11-19: 중간의 perturbation을 업데이트 하는 신호 $\rho$ 결과를 찾도록 binary search를 실행 하는 부분. 그 이유는 확률적으로 본 논문의 알고리즘은 궁극적인 목표를 벗어날 수 있는데, 이러한 binary search가 억제한다고 한다. 즉.. 이 부분이 모델을 더 잘 설명할 수 있도록 한다.
line 20: $\eta$ 반지름의 $l_2-ball$를 updated perturbation에 투영한다.
line 21-22: 작은 변동과 clip을 거친 분산 샘플에 대한 $\mathfrak{H}$을 추산한다.

perturbation의 $l_p-norm$은 인식이 불가능하게 만드는 적대적 설정으로 제한되는 반면에, 본 논문에서는 전혀 다른 역할을 한다. 반복적인 back-propjection과 clipping을 통해, 모든 입력 샘플에 대한 $l_{label}$을 예측하는 $\kappa(.)$에 큰 영향을 미치는 기하학적인 패턴 perturbation을 증폭시킨다. 밑의 figure 2에서 확인 할 수 있다. 그리고 정제를 통해 더욱 더 잘 확인할 수 있다.

*Perturbation refinement: * 질 좋은 패턴을 뽑아내기위해 Algorithm 2를 보면 적절한 구역에서 적응할 수 있는 filter에 집중한 기술을 볼 수 있다.

이 알고리즘의 핵심은 앞선 외부의 영향이 없다는 가정하에 perturbation의 정확도를 유지하는 것이다.
line 2: perturbation을 정제하기위해서 분류기의 convolutional base인 $\bar{\kappa}(.)$을 입력으로 넣는다.
line 3: 출력인 $\Omega$는 낮은 해상도의 2D signal을 가지며, 평균 signal $a$에 의해 축소된 것이다. 이 signal은 입력 perturbation에서 대략적인 salient region의 윤각을 보여주어, 본 기술에 유용한 spatial filter가 된다.
line 4: $\Phi(.)$는 평균 signal에 대한 'Otsu threshold'를 계산한다.
line 5: 이미지를 이분화하기위해 위의 $\Phi(.)$를 사용한다.
line 6: 입력 perturbation의 차원을 맞추기 위해 결과로 나온 이미지에 bicubic interpolation로 upsampling 한다. 그 뒤에 scailed mask가 perturbation에 적용되고 뒤의 valid dtnamic range에서 cliping 한다.
알고리즘 2의 출력은 알고리즘 1에의해추가로 처리되며, 필터링으로 감소 할 수있는 sailent pattern을 다시 강조한다. 최종의 perturbatin은 위의 두가지 알고리즘이 반복적으로 실행되어 계산된다.

5. Experimentation

5.1 Model explanation

Setup: $I$는 original image이고 $\bar{D}$는 ILSVRC 2012 validation dataset에서 256개의 이미지를 랜덤으로 샘플링한 dataset이다. mini-batch인 $b = 32$, probability threshold인 $\gamma = 0.8$ and perturbation norm인 $\eta = 10$ 이다. $\gamma$는 최종 perturbation에서 salient pattern이 확연하게 보이는 값으로 정했다. 높은 $\gamma$는 더 깨끗한 패턴을 보이지만 더 높은 계산량을 가진다. $\eta$의 경우 기존의 논문끼리 비교를 통해 정했다. 하드웨어는 Titan V gpu with 12 GB RAM을 사용함.

perturbation을 구하기위해, Algorithm 1을 먼저 실행한다. (desired $\mathfrak{H}$) 그 후에 refinement를 위해 algorithm 2 를 실행한다. 그 후에, algorithm 1을 실행하지만 300 iteration 전까지 매 50 interation 마다 refinement (algorithm2) 를 실행한다.

Salient visual features: 본 논문에서는의 공격은 이러한 perturbation의 signal을 통해 target label들의 salient feature들을 발견할 수 있도록 한다. 그림 3을 보면 확연하게 볼 수 있으며, 어떤 perturbation이 없더라도 패턴이 나타남을 알 수 있다.

위의 그림을 보면서 먼저 '사람-이해 의미론적인 것이 출력 뉴런에 연결 되는 것'에 대한 답을 내릴 수 있다. 즉, 잘 모르는 모델을 가지고 label의 output layer을 봐야할 때 유용하다. 두번째로, "분류기로 부터 해당 클래스를 구분하는 특징이 어떤 기하학적 패턴을 가지는가?''에 대한 답을 내릴 수 있다. 그림을 보면 사람 개념과 유사하게 패턴을 잘 정렬한다. 즉.. 딥러닝이 사물을 인식하는 것과 사람이 사물을 인식하는 것과 유사하다고 볼 수 있다.

Diversity of the salient patterns: 그림 3에서 다른 모양으로 나타나는 이유는 seed를 다르게줘서 그렇다. 그리고 salient map을 통해서 deep learning model 또한 사람이 사물을 인식하는 것처럼 인식한다고 단언할 수 있다. $\bar{D}$는 독립적으로 생성해서 실험을 진행 하였는데, 이러한 패턴들이 visual model을 통해 만들어지고 보여진다. (image generation and image classification)

Region specific semantic: 이미지 공간의 특정 영역과 관련된 모델 의미론을 추출 할 가능성에 대해서도 탐구했다. 이렇게하면 개별적인 샘플의 기울기가 지정된 영역에 대해 동일한 방향으로 이끈다. back-projection으로 해당 영역의 신호를 강화하는 반면 다른 영역의 약한 신호는 정제를 통해 억제된다. 모든 샘플에 대해 관심 이미지 영역을 64x64 패치로 대체하여 모방하는데, 모든 패치 픽셀은 샘플의 평균 픽셀 값으로 생성된다.

그림 4는 지네를 라벨로 랜덤한 영역에 넣어서 salient feature map을 보인 결과이다. 보는 것과 같이 공격은 특정 영역근처에 더 집중적이다. 흥미롭게도, 대상 라벨의 유사한 차별적인 특징을 일관된 방식으로 서로 다른 영역에 연관시킬 수 있으며, deep representation과 인산 인식 사이의 차이점이 없어 보인다.

*Patterns for different models: * 위의 그림 4는 resizing을 한 뒤에 보여준 패턴이다. 그러나, salient visual feature들의 나타남은 deep visual classifier에서 나타나는 일반적인 현상이다.

그림 5에서 보듯이 perturbation들은 모든 모델에서 해당 라벨의 특징을 명백하게 묘사한다.

해당 모델에 대해서 여러 모델들의 높은 confidence는 추출된 패턴들이 해당 class의 구별가능한 visual feature들로 잘 보이는 것으로 나타낸다. -> 즉... 어떤 모델에서든 추출한 visual feature들은 다른 모델에서도 잘 작동시킬 수 있는 visual feature들을 뽑아 낸다는 것이다.

5.2 Leverage in low-level tasks

Santuraker et al 41은 이미지 생성과 인페이팅에서 자신들의 모델을 증명햇으며, 적대적인 robust deep calssifier들을 사용했다. 또한, 강력한 분류기를 위해 계산된 적대적 perturbation에서 salient visual feature의 존재에 대한 논문이다. 위의 논문도 우리의 발견과 관계가 있다. 성공적으로 모델을 설명할 수 있을 뿐만 아니라 SOTA를 달성했다.
결과에 대한 개선점을 증명하기위해 41과 똑같은 budget과 평가 과정을 사용하였다. $\bar{D}$를 샘플링 할때는 다중 가우시안 분포 $N(\mu_1,\Sigma_1)$를 사용했으며, ImageNet에서 가져왔다. 계산을 위해 다중 가우시안 분포는 원본의 이미지들의 4x downsampling을 사용하였다. 랜덤으로 256개 분포 샘플들은 네트워크 입력과의 일치를 위해 나중에 업샘플링되고 $\bar{D}$에 사용된다. 전체적으로 이미지 프로세싱은 했지만, refinement step을 제외하였다.

5.2.1 Image Genearation

적대적 공격의 맥략에서, 생성된 이미지는 seed image의 적대적인 예시이다. 다양한 시드, 텍스쳐 세부 정보 및 명확한 의미 일관성으로 생성된 이미지의 다양성은 강력한 분류기가 분류 이상을 수행 할 수 있음을 의미한다.

5.2.2 Inpainting

다음의 task를 해결하기 위해 변질된 이미지를 binary mask로 알아보게 만든 seed로 다룬다. robust classifier parameter들을 고정하고 밑의 loss를 최소화 하는 것으로 목표로 한다.
$$
L(p)=\mathbb{E}[\mathcal{J}(\mathfrak{F}_ p,l_{target})+\beta(p\odot(1-F))],
$$
$\mathfrak{F}_p = \mathfrak{F}\ominus p,$ $\mathcal{J}$는 cross-entropy loss 이다. $\beta=10$으로 고정하며 실험적으로 얻어낸 scaling factor이다. 위의 loss function은 perturbation 신호가 제한 없이 변질된 이미지를 다른 구역과는 자유롭게 해결하기위해 만든다.

41과 비교한 그림이며 같은 perturbation budget 인 $\eta=21$를 사용했다. 시각적으로도 잘 생성하고 더 좋은 결과를 가져온다.

5.2.3 Interactive Image Manipulation

대충 그린 스케치로 부터 그림을 생성하는 기술을 attacking/fooling robust classifiers로 해결할 수 있는 가능성을 41에서 제시했다. 논문의 기술이 더 적합함을 보였다.
다중 가우시안 분포를 사용하여 만들었지만 refinement 과정이 포함되어있다. 결과는 밑의 그림에서 확인 할 수 있다.

위의 3가지 기술 (generation, inpainting and manipulation)을 통해 perturbations이 보통적으로 모델을 바보로 만들 뿐만 아니라 저자들이 알고자하는 방향에 대한 확신을 준다고 한다.

6. Conclusion

본 논문은 모델을 바보처럼 만드는 것이 아닌 설명을 목적으로 한 attack의 첫 논문입니다. 작은 변화를 계산하기위해 공격은 모델의 cost surface에 대해 stochastic gradient search를 수행하여 특정 대상으로 분류 될 이미지의 '분포' 로그 확률을 높인다...(?) 반복적으로 기울기의 back-projection 와 adaptive attention와 함께 재정의 함으로써, 논문의 공격은 분류기의 salient로 여겨지는 작은 변화인 기하학적인 패턴을 발견했다. 현실적인 이미지생성, 인페이팅 그리고 interactive image manipulation은 모델에 대한 공격의 nature을 알아냈으며, 사전의 SOTA에 대한 새로운 분류기 활용을 발견했다.